Last Modified: 2023-Jun-29

Remember to right click->"open image in new tab" for small images

Índice

  1. The cell graph
    1. Shortest path
    2. Steps to solve the shortest path
      1. Point to Line Algorithm
    3. Modifying the requirement
      1. Shortest path withing allowed roads
  2. A better algorithm
  3. Future solutions:
  4. Semi-conclusion
    1. Voronoi - A better way to define a cell’s network and range

Wed May 3 04:04:51 PM CEST 2023

The cell graph

In order to simulate the cell network, we need realistic data of base stations’ positions. The closer we have:

Data from opencellID integrated.

There’s a range field, but it’s 1km in most of the samples, which results in cells being at one jump from each other.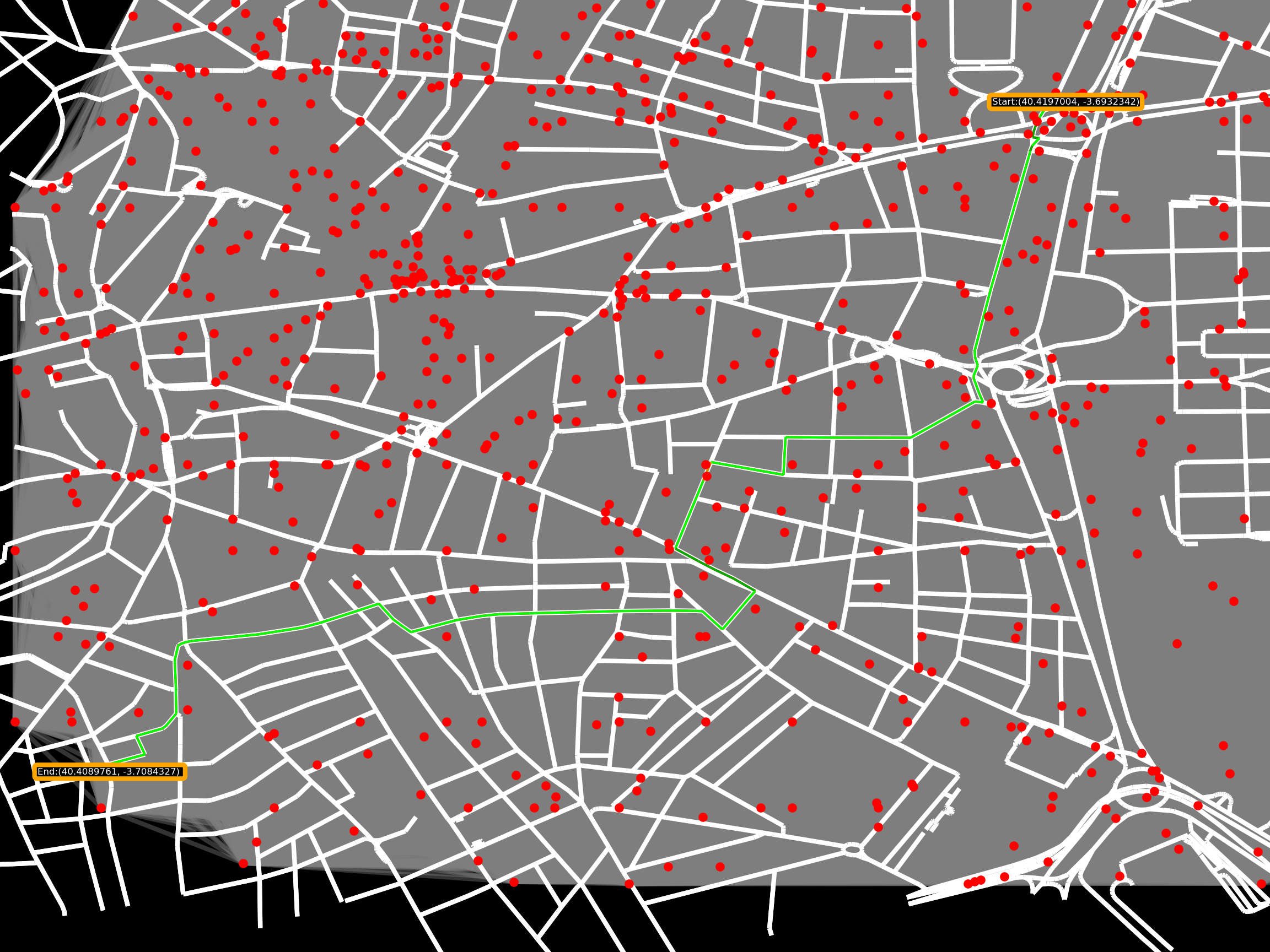

Using sphere of influence algorithm :

But still, there are some islands, I will apply the same sphere of influence, but with the second closer node as a range d6918b8

A better graph is obtained, at first glance, no isolated graphs. Just in case, I will search for them dd6bf45.

> python main.py
...
No Unreachable nodes in base station graph
...

Sun May 7 05:21:53 PM CEST 2023

Shortest path

The sphere of influence algorithm doesn’t guarantee that all of the map will be covered by the ranges of each node.

TODO - better way to make the graph

Steps to solve the shortest path

  1. Choose the origin and end nodes Done
  2. Find the closest base station to each node Done

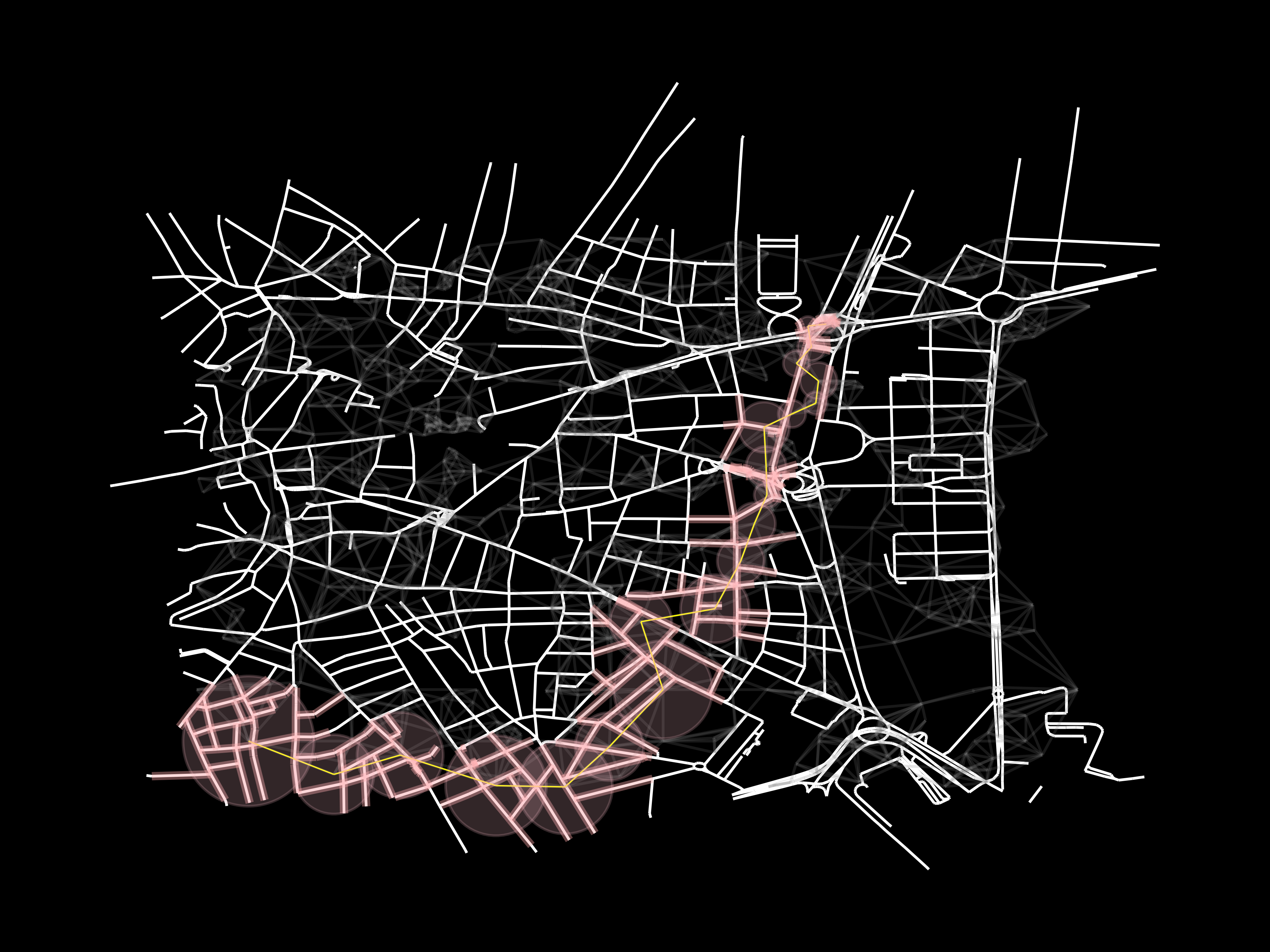
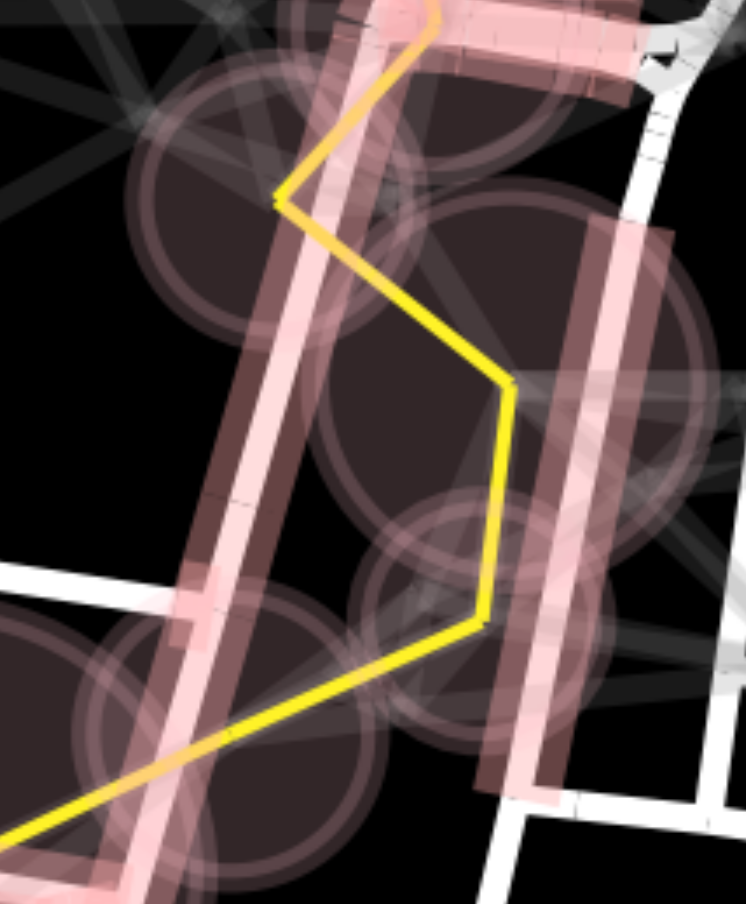
  3. BSpath(in transparent yellow) - Find shortest distance in the base station graph, Done 7661ee4 This way, we minimize the number of cells required, in the real life scenario, each cell will have a limited number of clients with the requirements needed for a remote drive. Hence, the less cells required, the more hypothetical cars/travels will be able to drive/perform at the same time

     cShPath=nx.dijkstra_path(Gt,bSStart,bSEnd) #weights = 1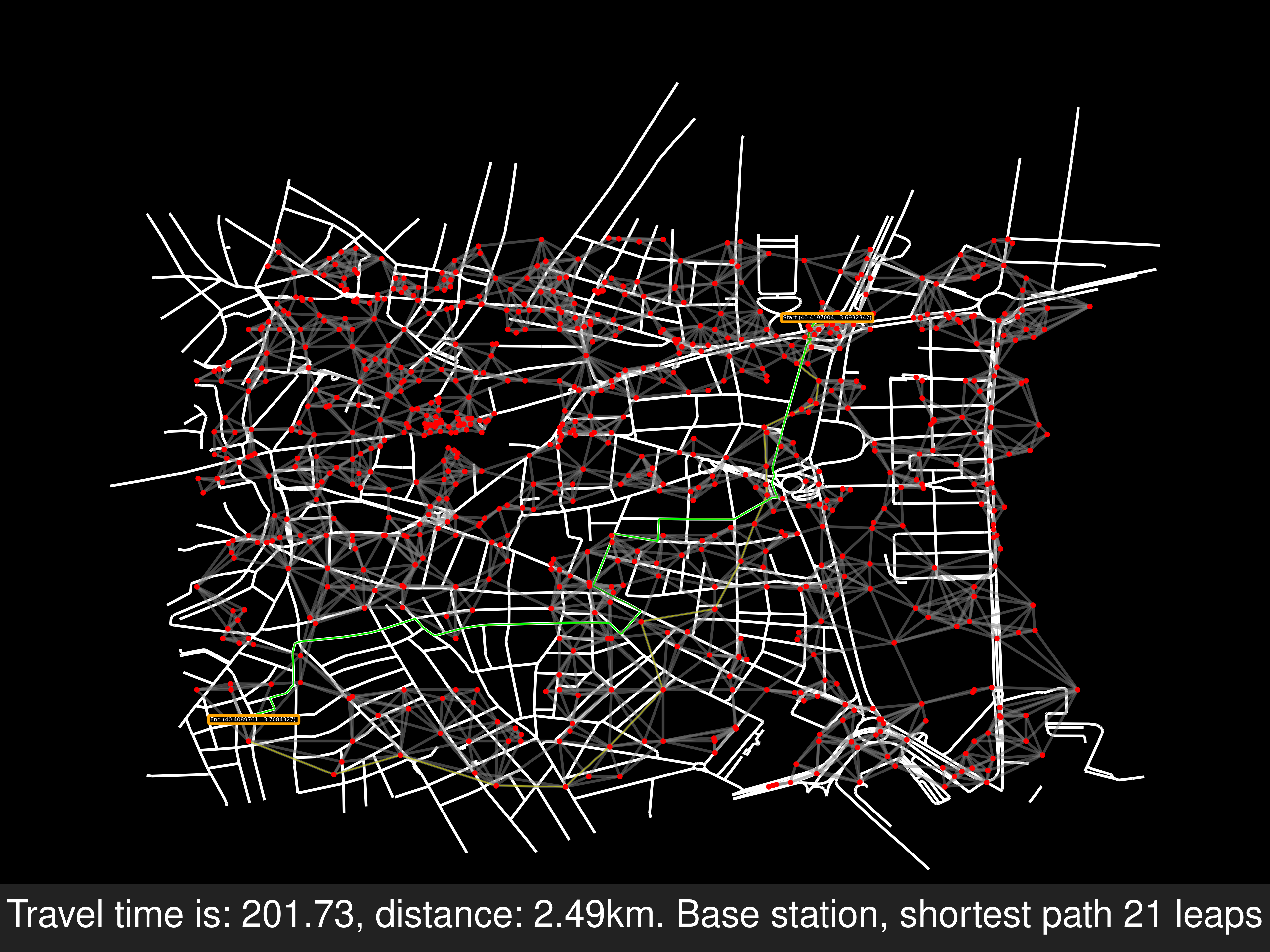

    Telefonica, orange and vodafone. From left to right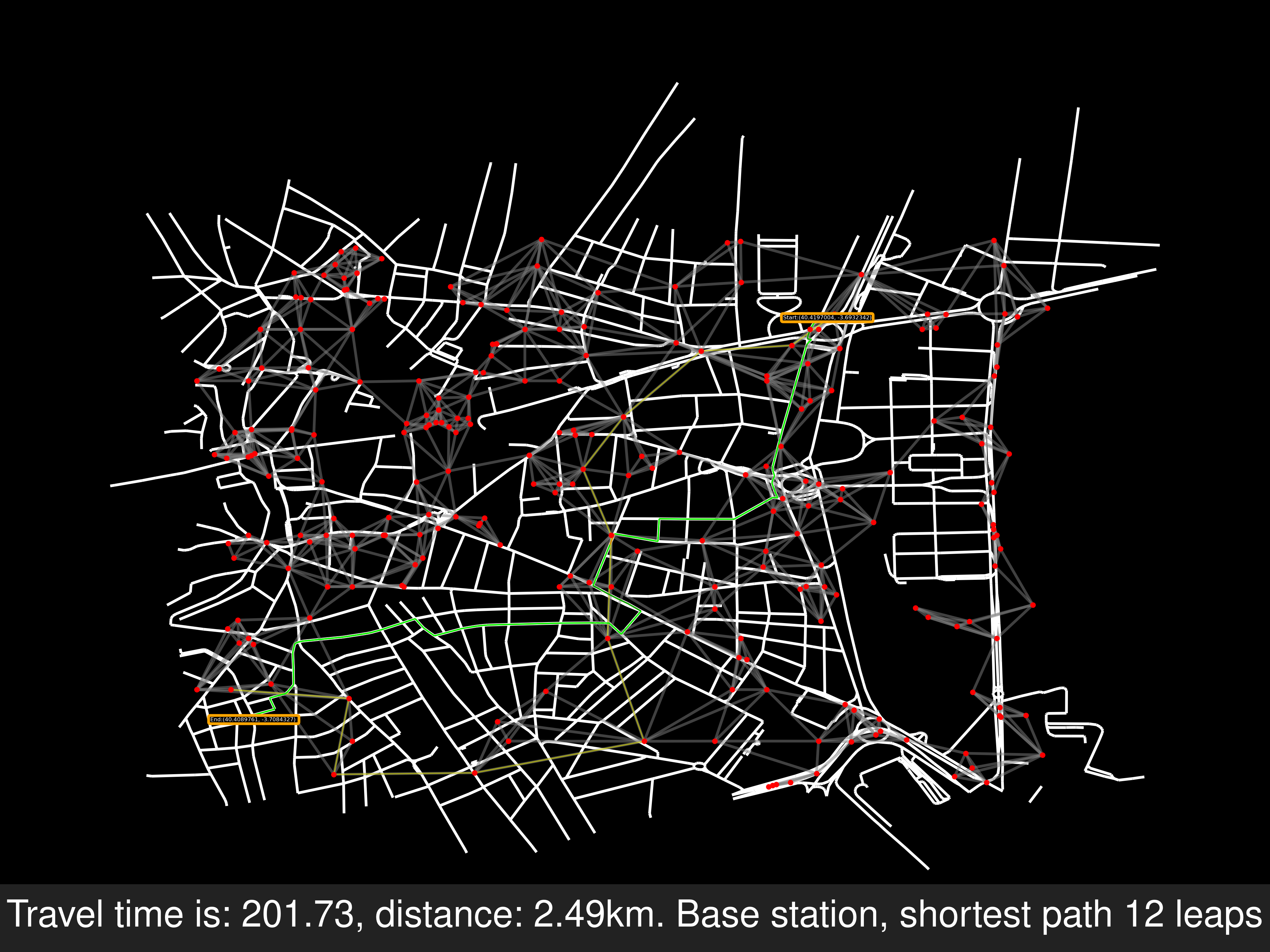

  4. Add a field to each road, ¿¿distance to the closer base station in the shortest BSpath ??. Discard roads outside of each base station’s range TODO
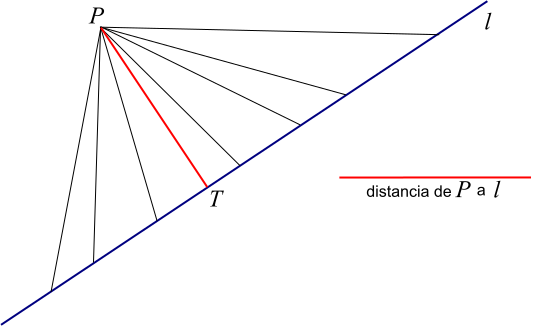
  5. Calculate the shortest road route with the updated weights, TODO

    Point to Line Algorithm

    As in the image below, I will get the distance for 5 points per edge and discard the way if the point is outside of any cell’s range

    Drini, Public domain, via Wikimedia Commons

    Because the range was defined when the sphere of influence was applied, if there are cells very close to each other, the range will be defined very short, hence, a voronoi-like distance, not overriding the range, instead of sphere of influence will be used in another example

Mon May 8 08:22:52 AM CEST 2023

The requirement in points to line algorithm is too restrictive, as can be seen, a path from origin to end in the road graph can’t be found, this isn’t neccesarily bad. We would just need to calculate another path within the cell’s network.

f74f1b8

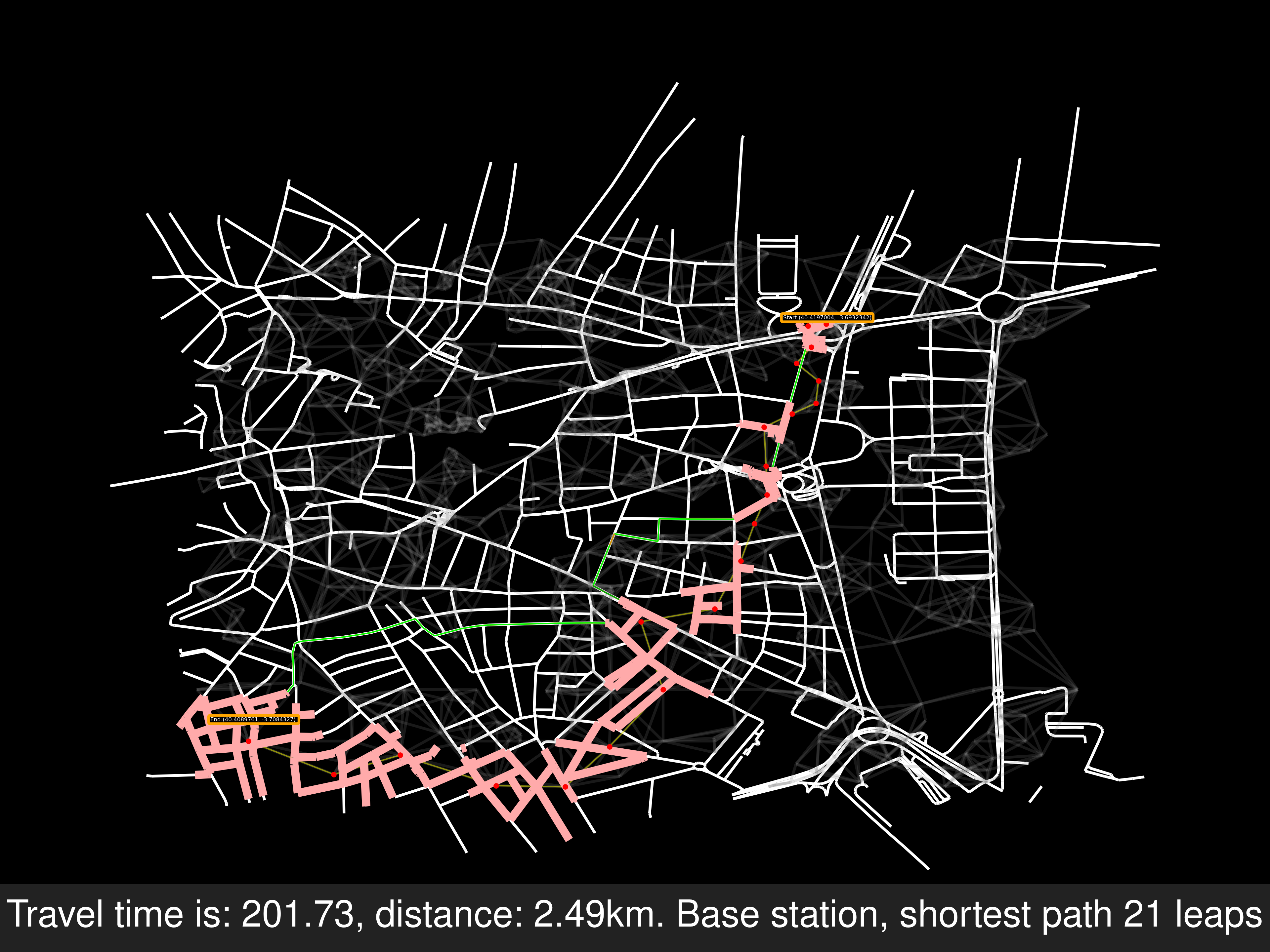
Modifying the requirement

08d9f71

Before adding an algorithm to find another cell network, I will modify the requirement soi. A way is acceptable, if any point within a road is inside the cell’s range

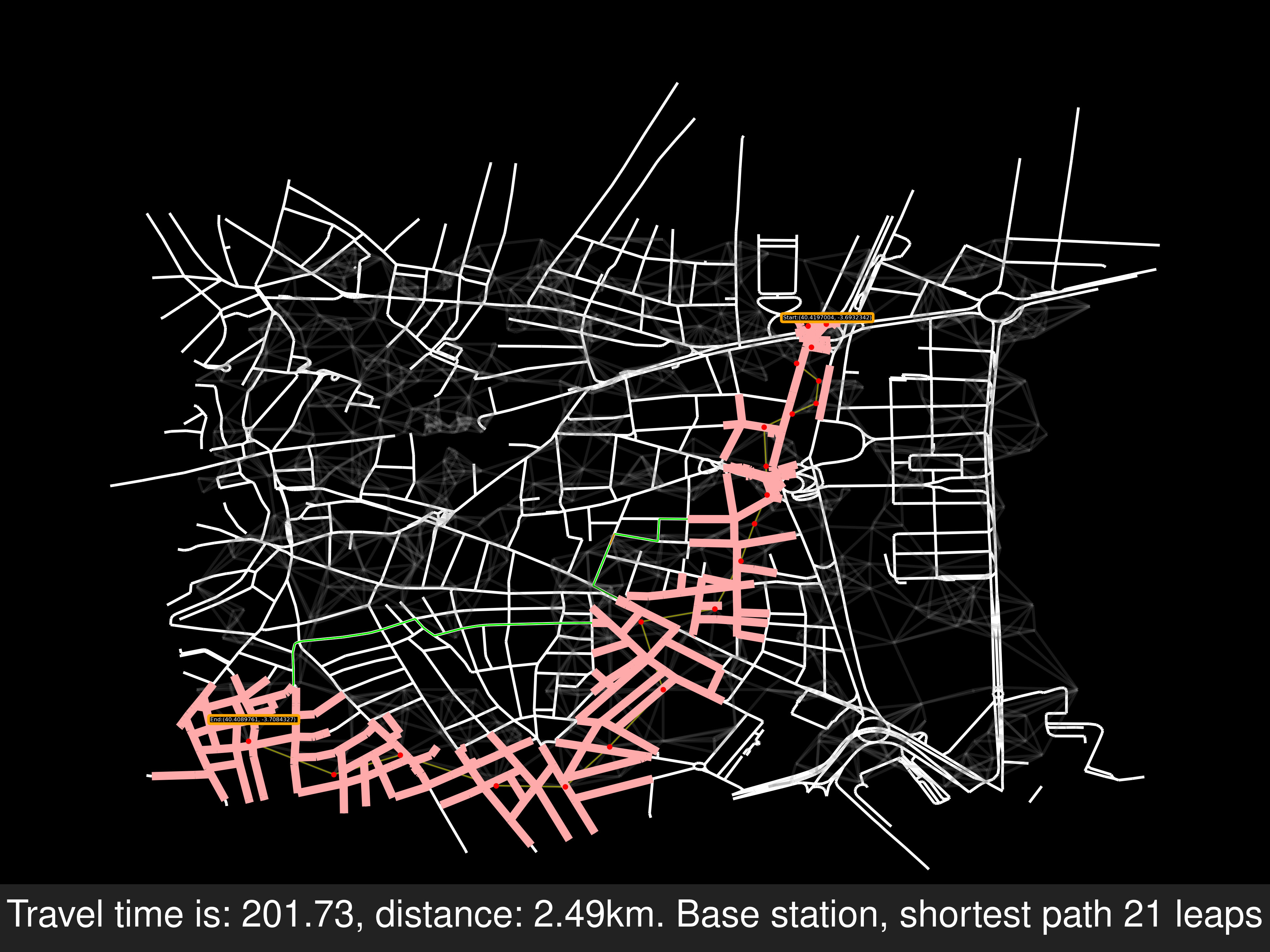
Shortest path withing allowed roads

From the initial steps and the modified condition, the initial and final road nodes will be inside the allowed roads. This should be straight forward, it isn’t

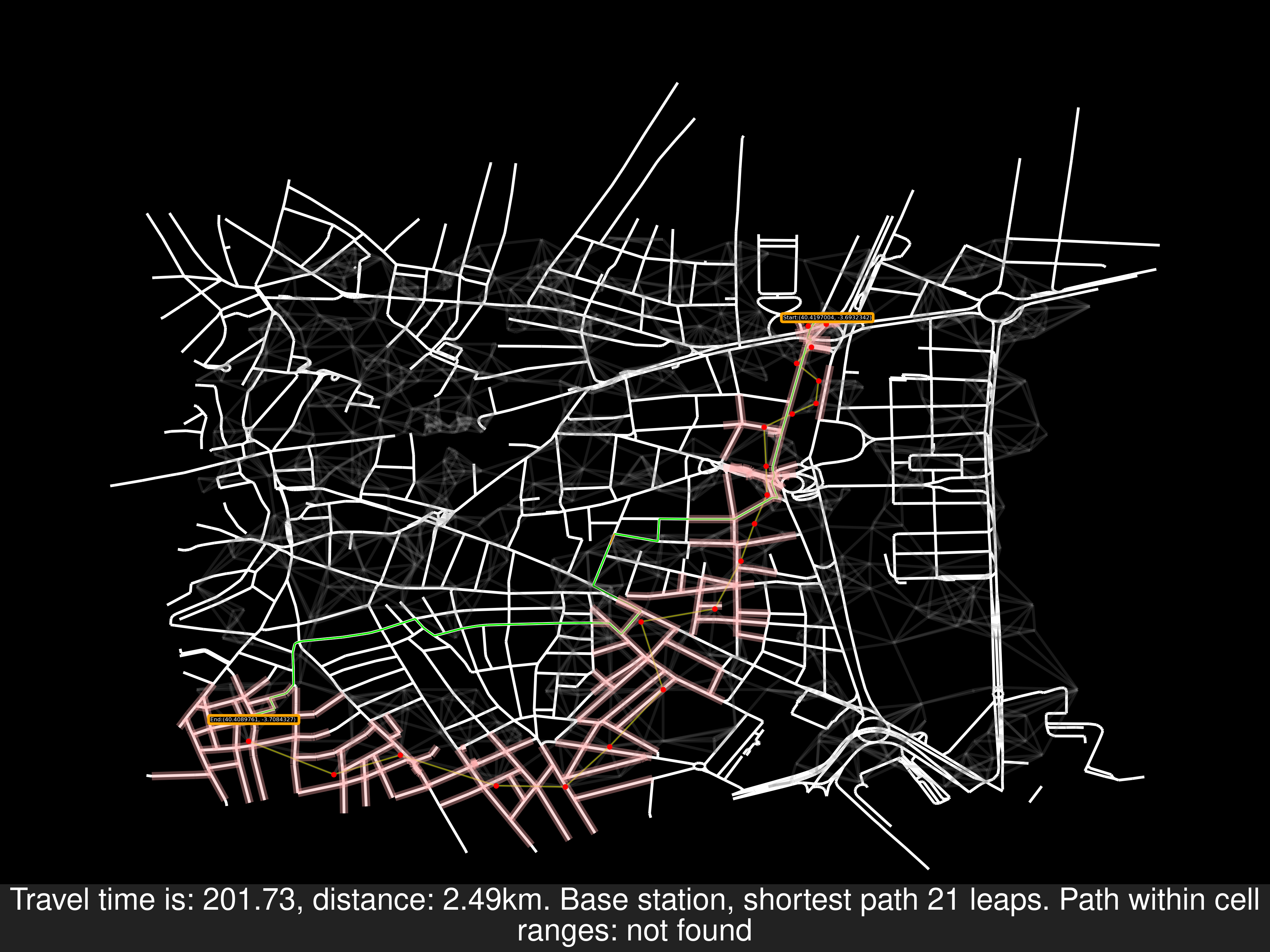
Other examples of random routes, one of them disproves that the starting node will necessarily be covered by a cell area: As a reminder, these problems have their origin in the SOI algorithm

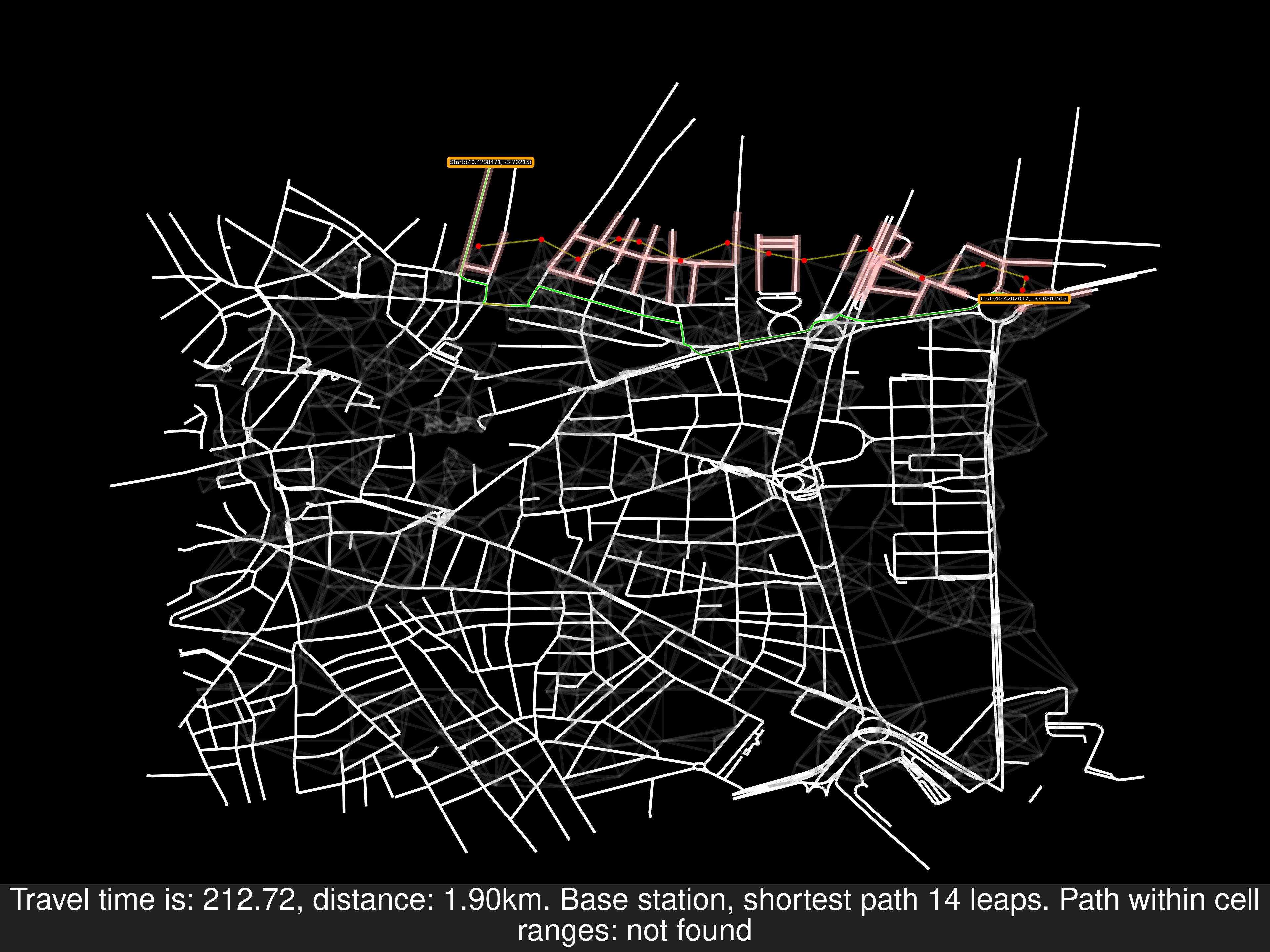
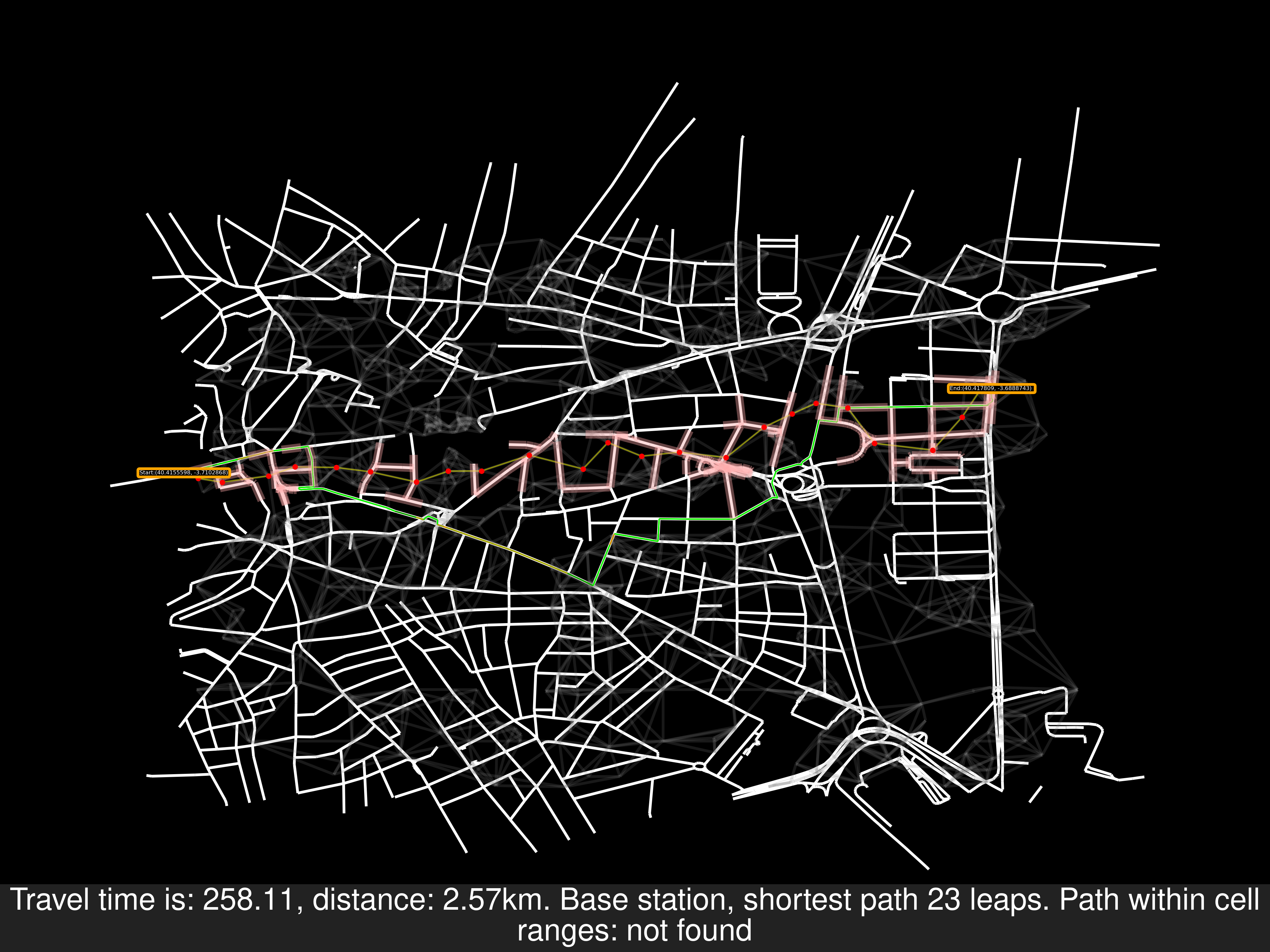
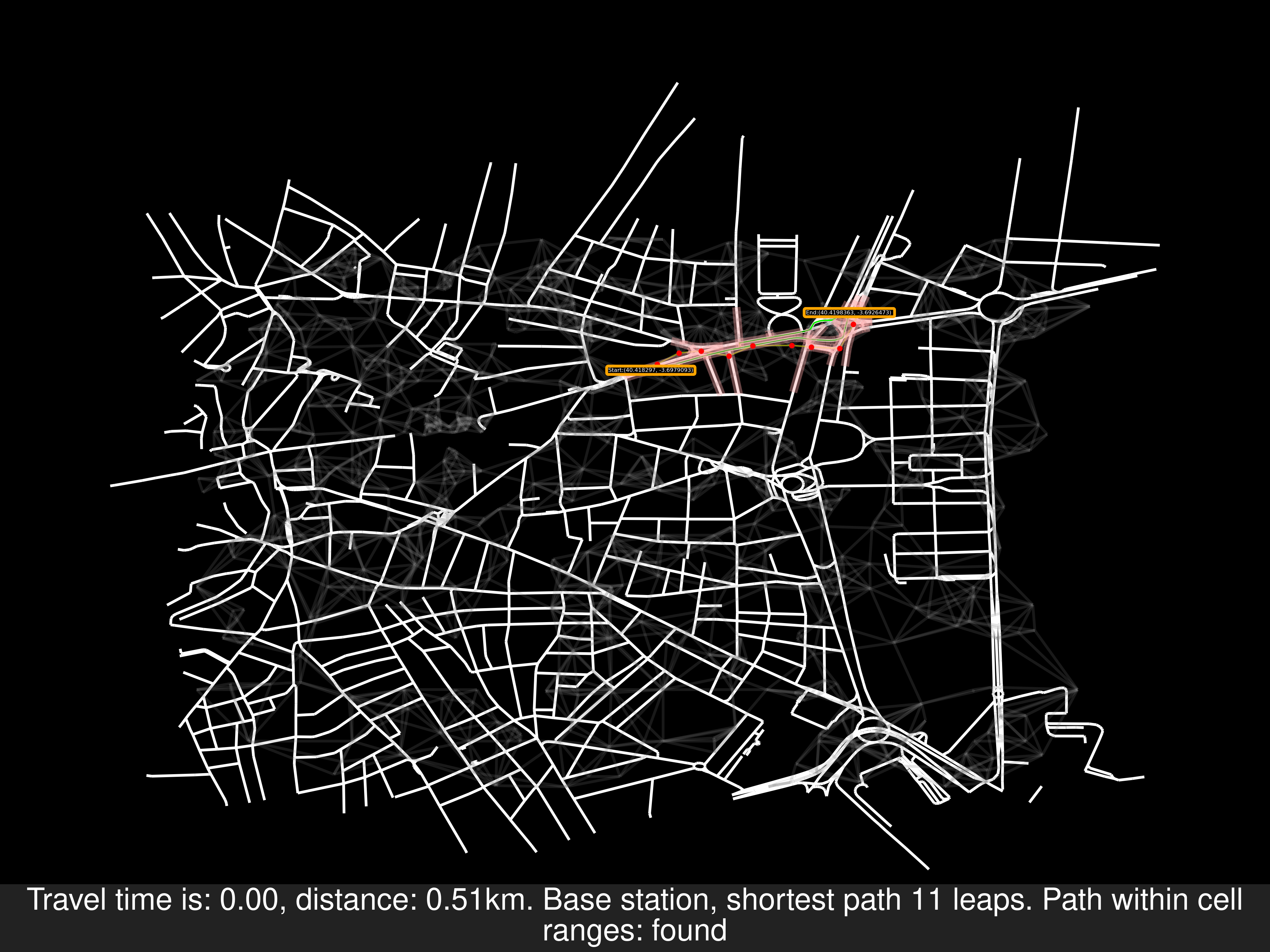
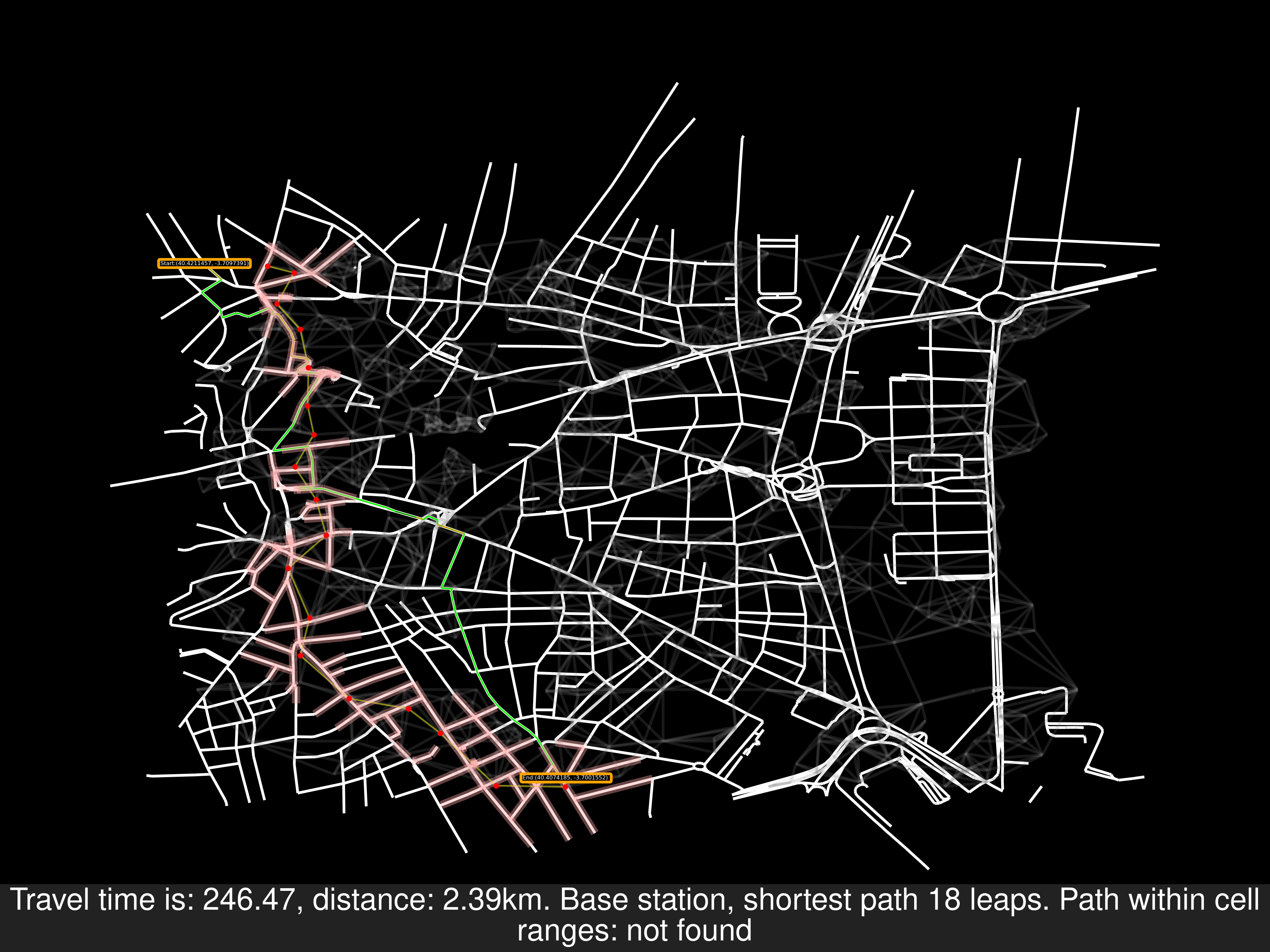
Sooner or later this would appear, there’s a gap in the coverage of the cells therefore a better algorithm is needed.

A better algorithm

As seen in the data, most cells are close to roads, it’s very likely that the gap in the coverage between two cells will be 1 or 2 cells away from being circumvented, it doesnt make much sense to perform the shortest path between the origin and end cells.

shortest_cell_route=[ cell0, cell1, cell2, cell3, cell4]
...
move_inRoad_from_to(cell0,cell4)
    ...
    //Can't move from cell1 to cell2 through the roads
    remove_edge_between(cell1,cell2)
    new_route=find_shortest_route_between(cell1,cell2)// or just find a new route
    shortest_cell_route=[cell0,cell1,cell5,cell7, cell2, cell3, cell4]
...

Wed May 10 10:26:42 PM CEST 2023

5797efa

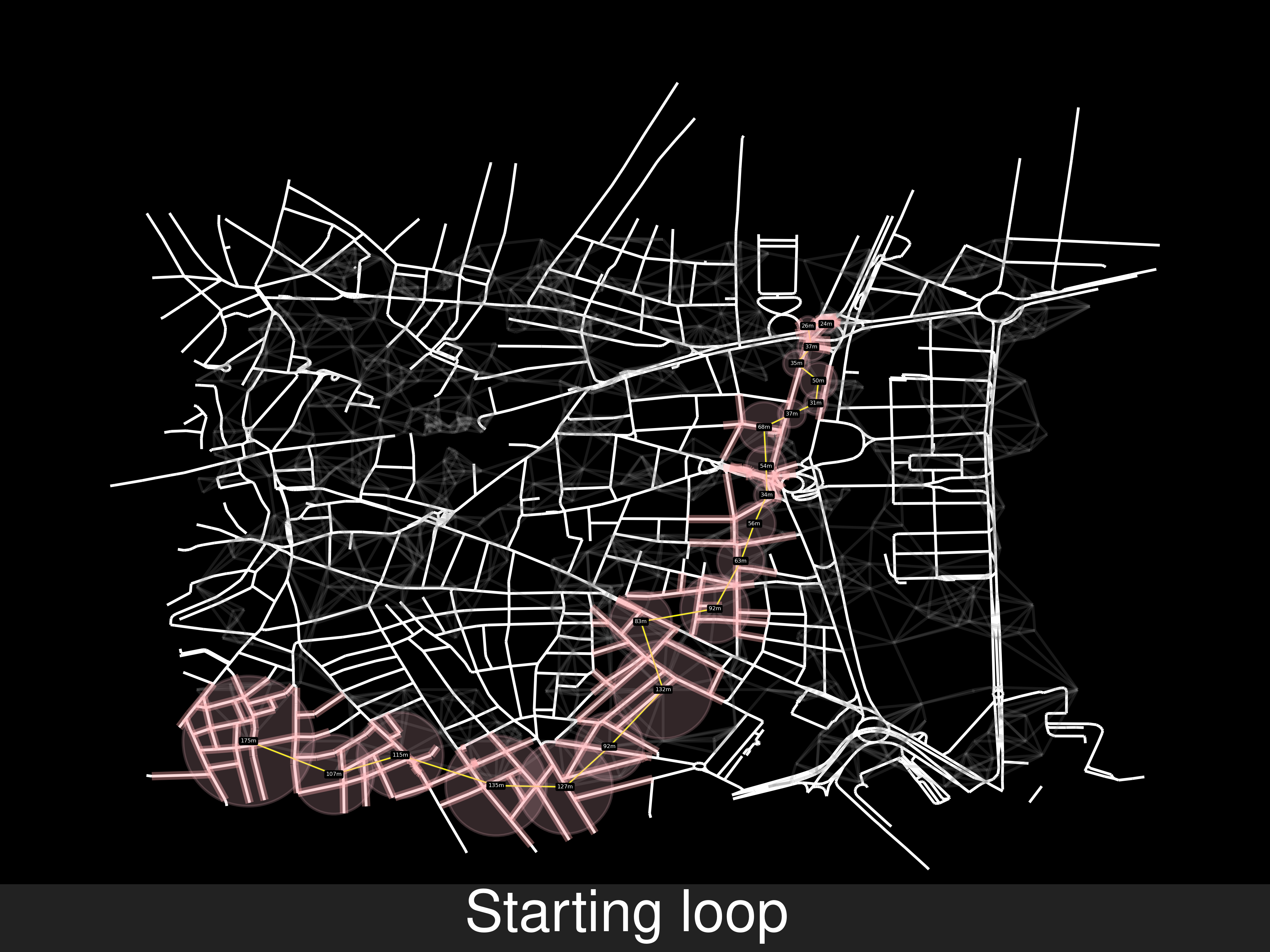
Gif with the sequence of steps, it’s 26MB, this page is big enough 😼.

  1. This approach doesn’t work that well.find_shortest_route_between doesn’t prove there’s a road path from where the car leaves cell0, joins and leaves cell1 and can join cell2. For that we would need to find the shortest route from some node of cell0 and some node of cell2, then cell3… until the last node

  2. Anyway, I will just find the shortest path between cel0 and cell4, instead of just the two cells unreachable cells. Now there’s another problem, yes, we know whether the starting node can reach the ending one, but we can’t pinpoint which pair of cells have unreachable nodes.

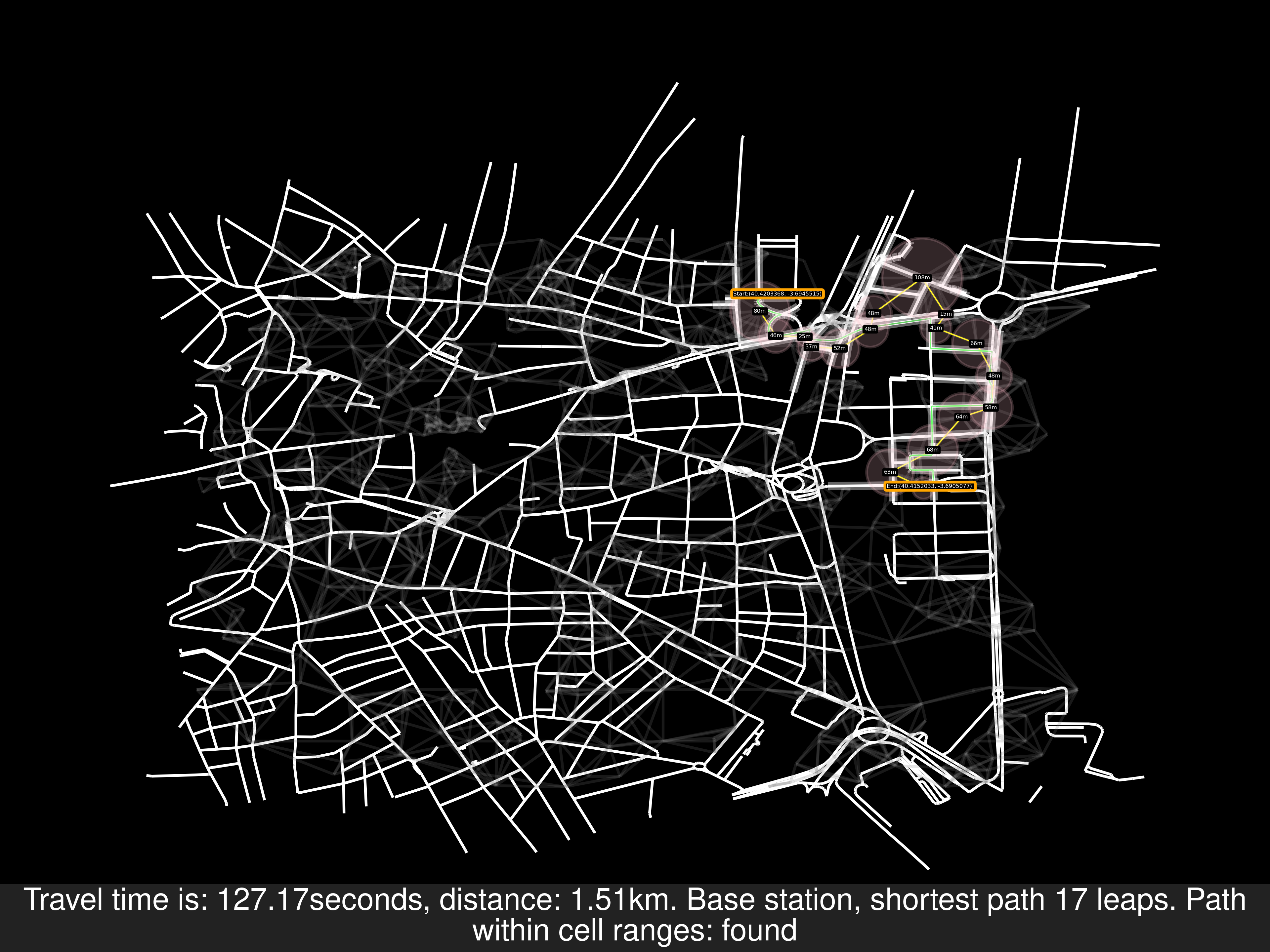
Merging both solutions: 3b887d3

  1. Example A of route solving

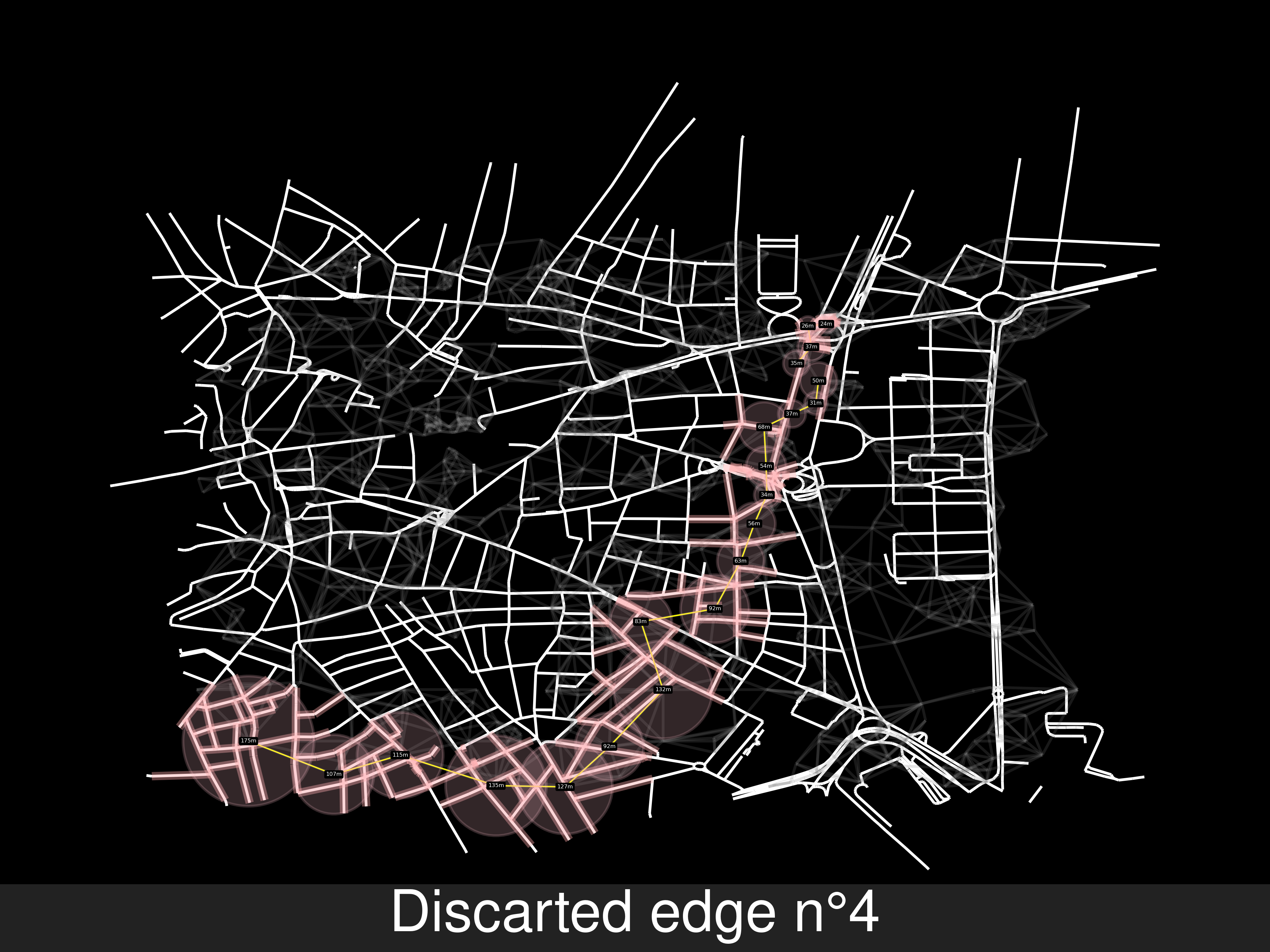
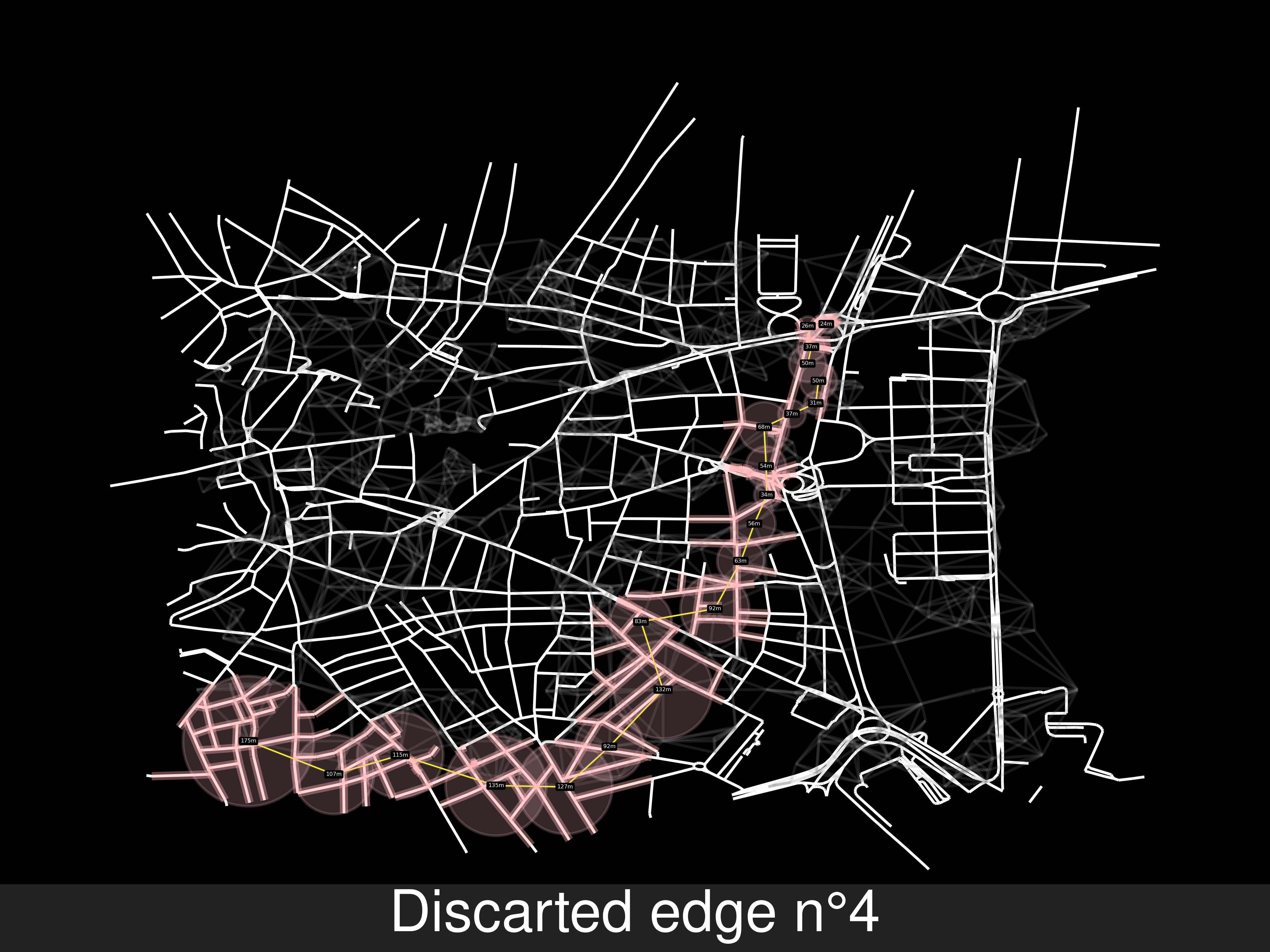
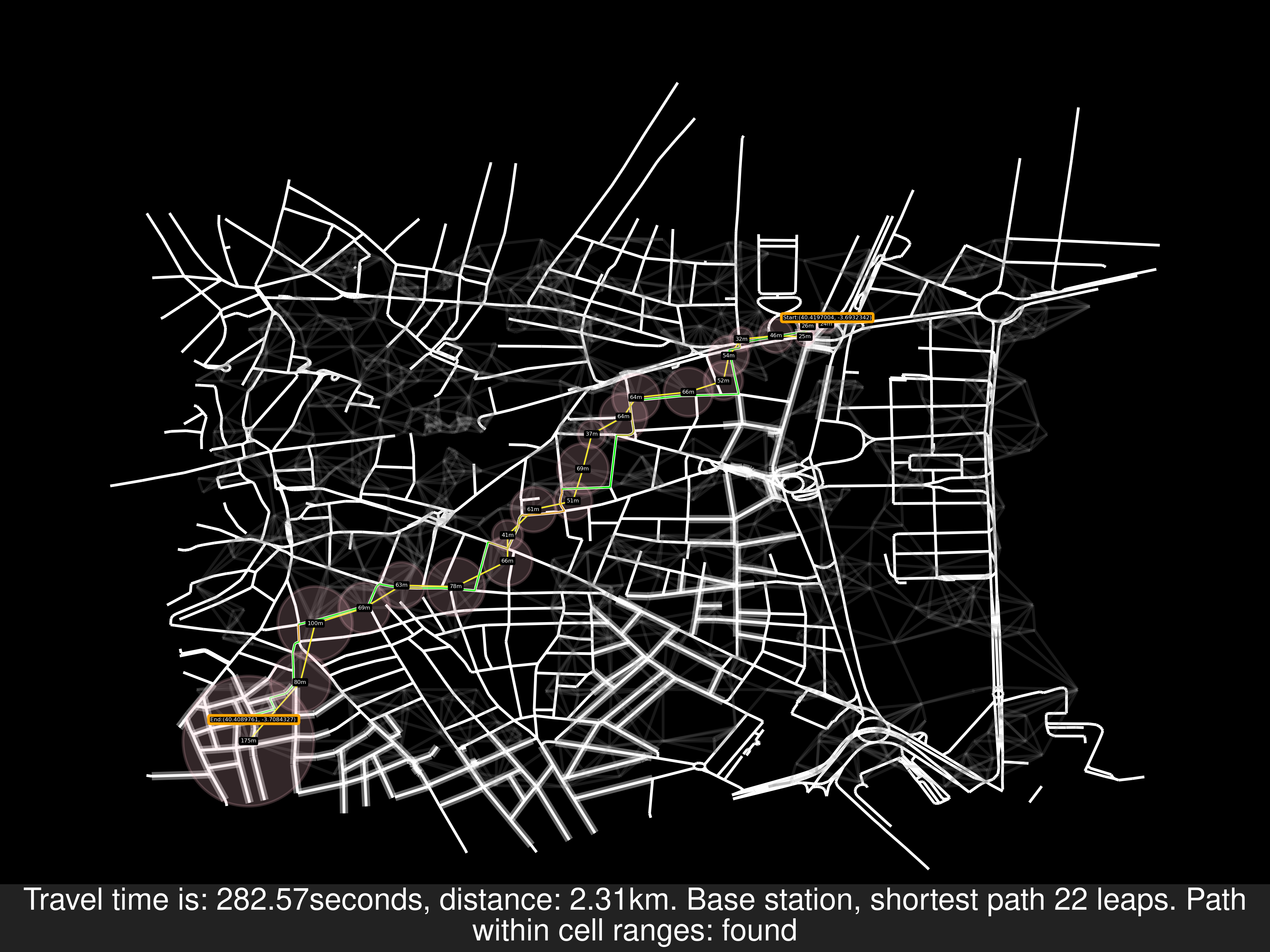
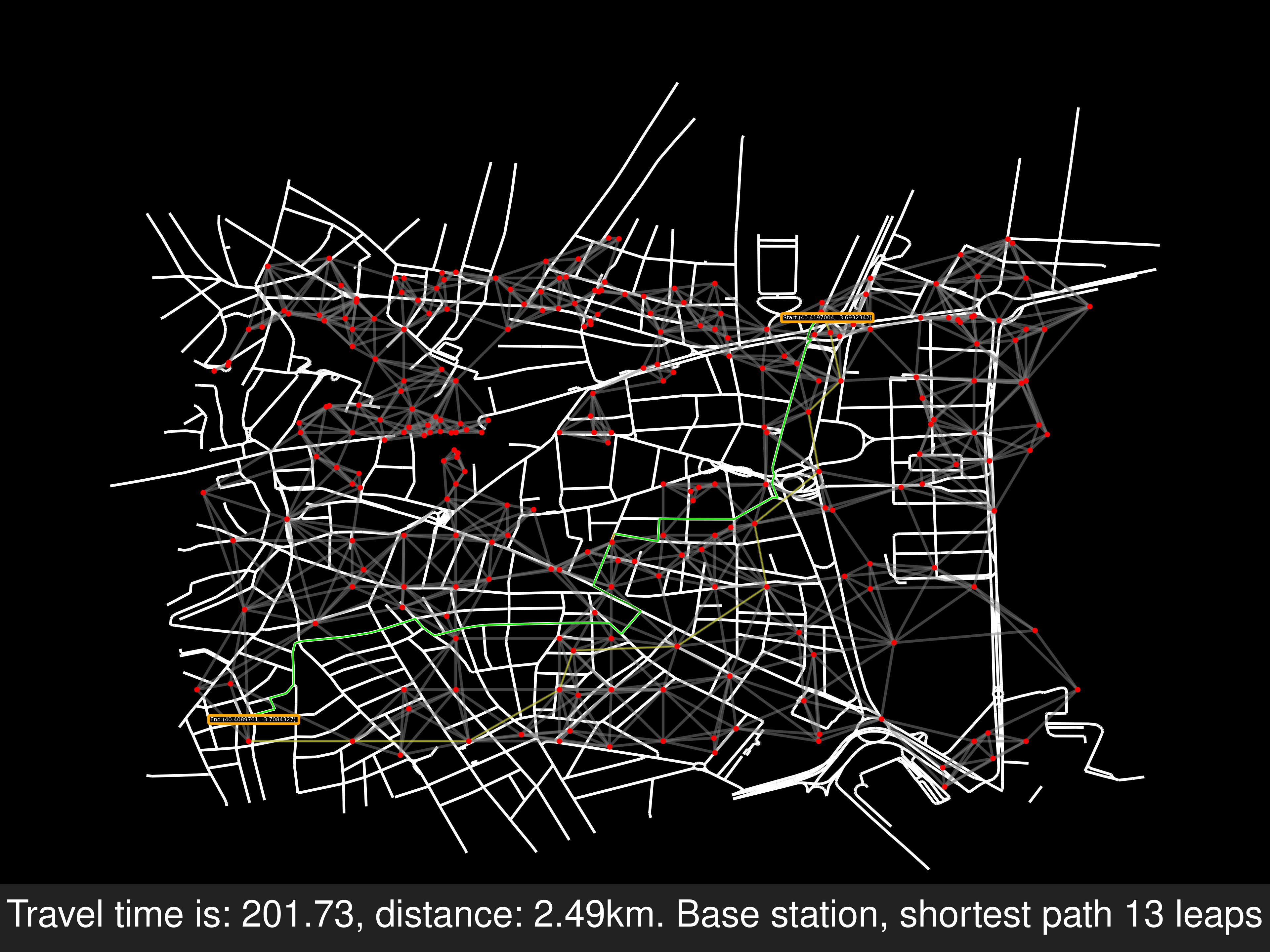
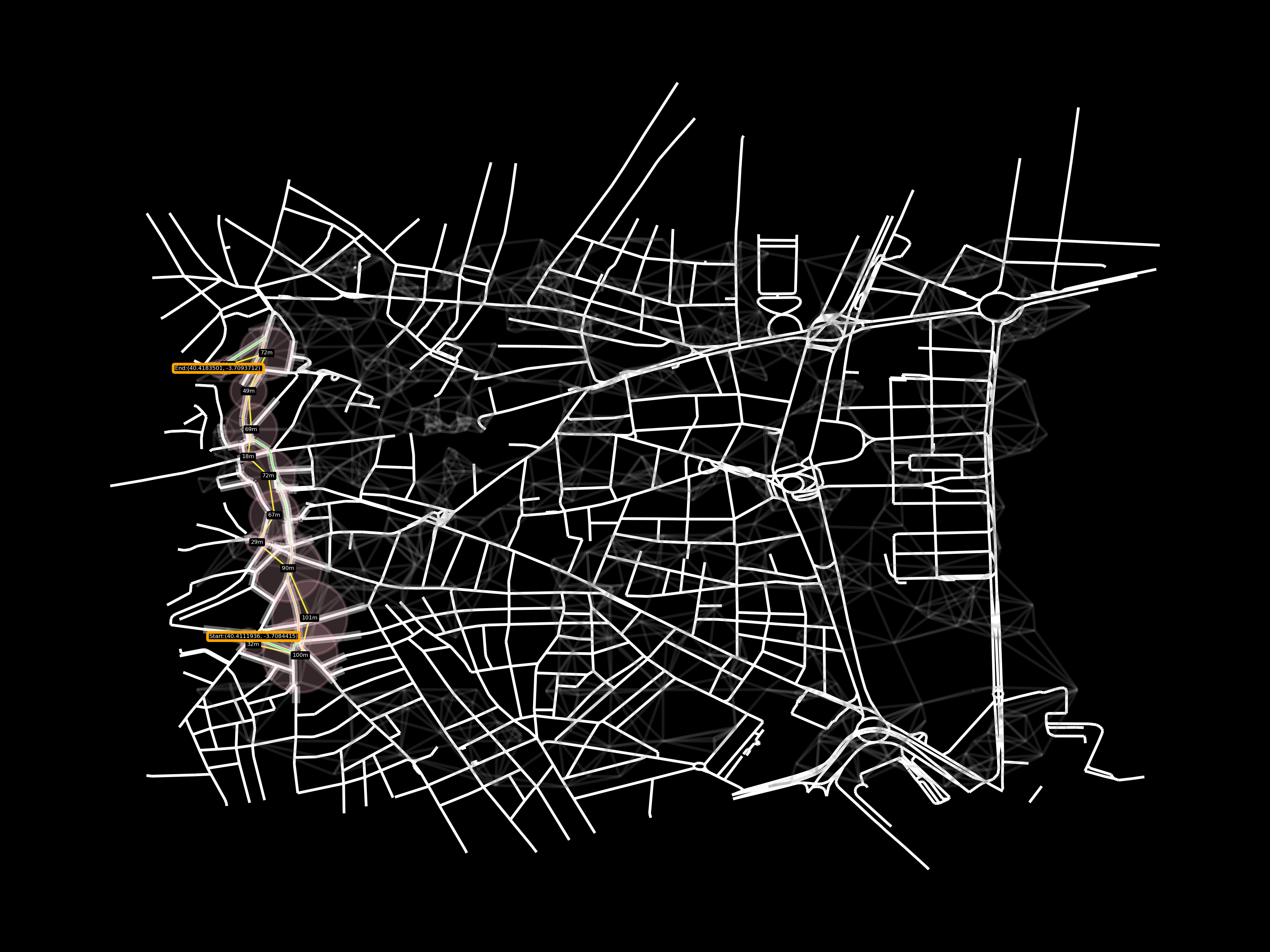
  2. Example B of no route solving, the end node is in another road. But because there’s a path between two random points of the last and second last, but not exactly from the source to the end. Will add the points in the labels of the pictures, for replicating these errors

    Other random starting and end nodes

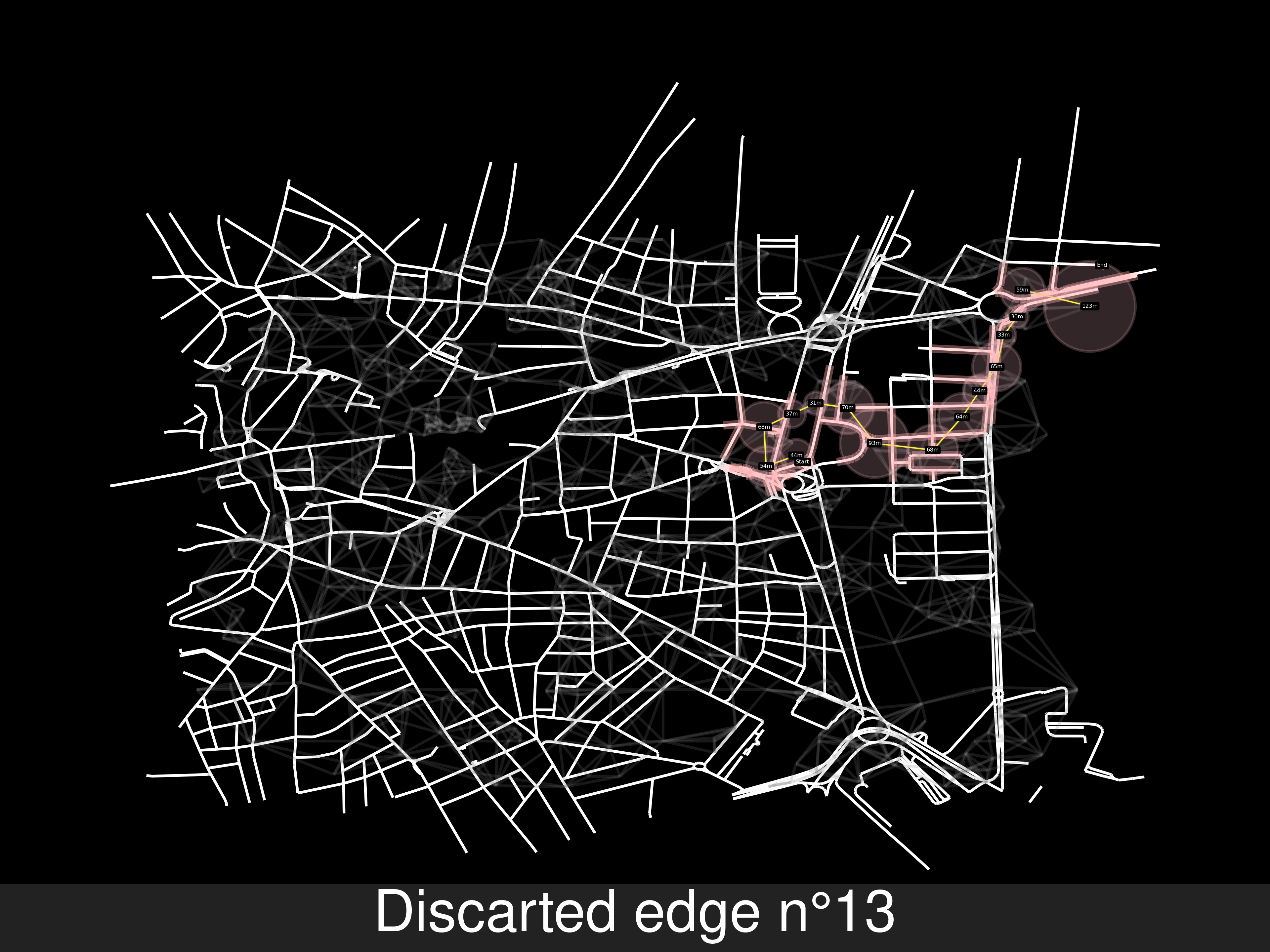
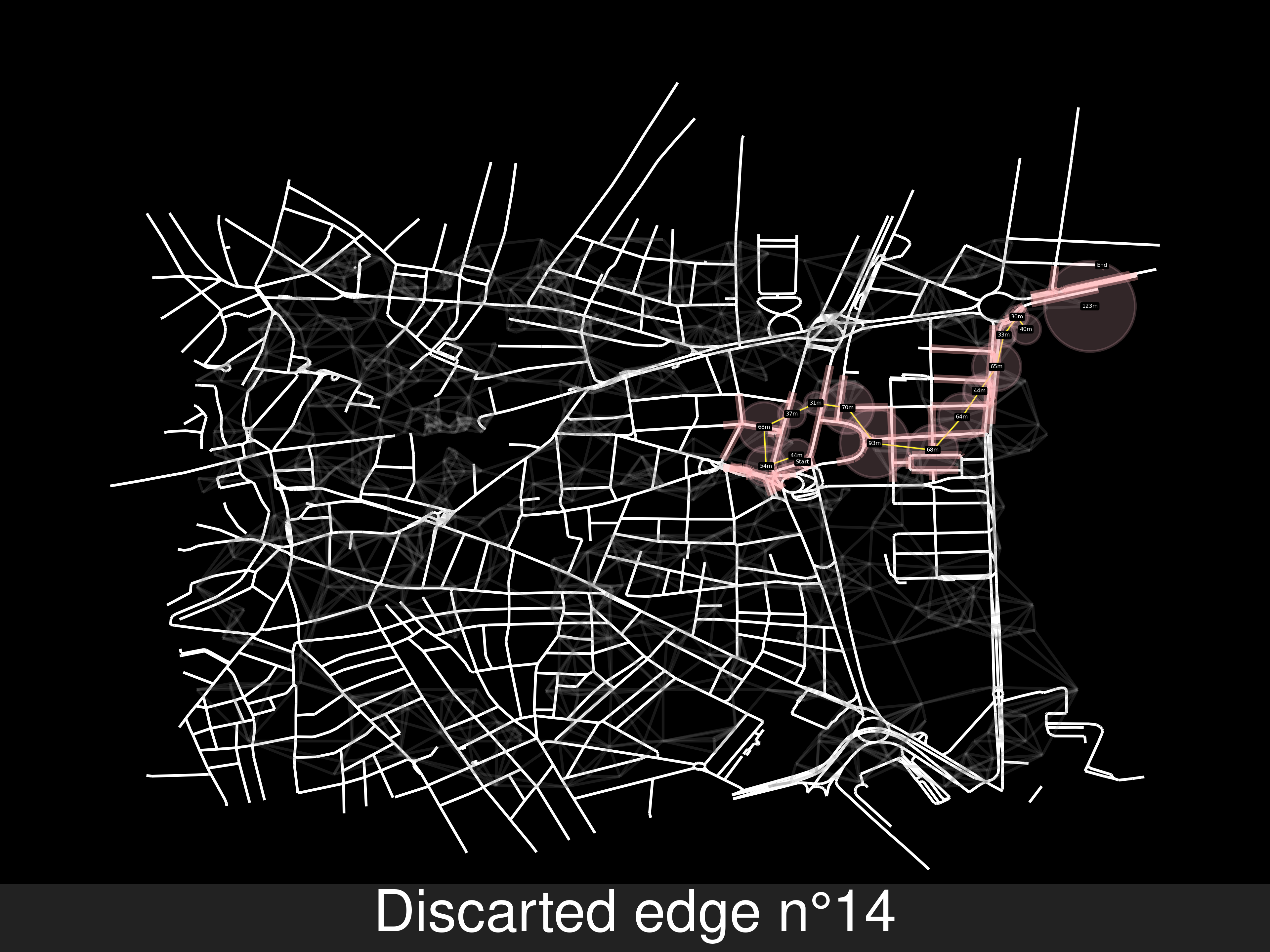
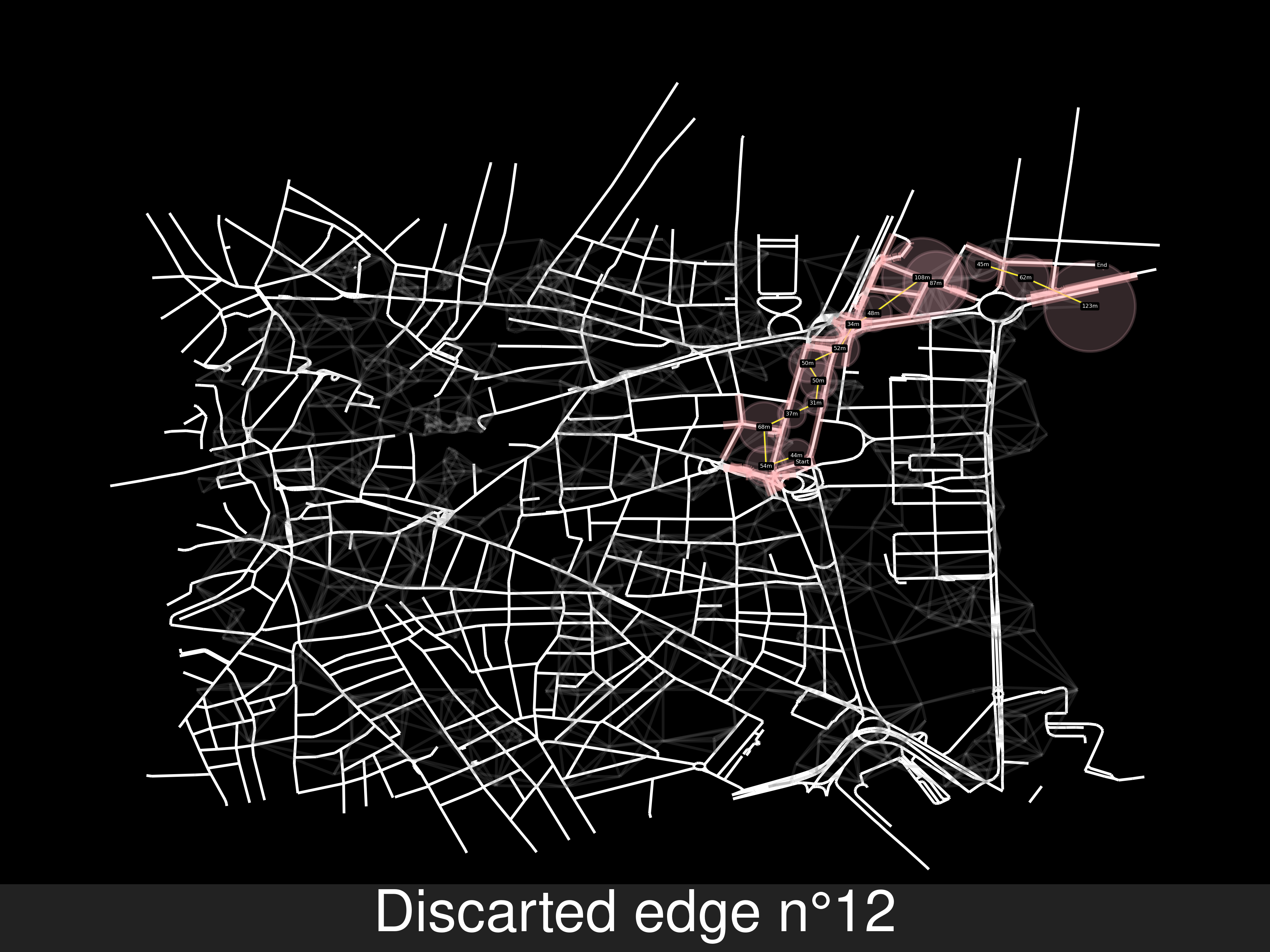
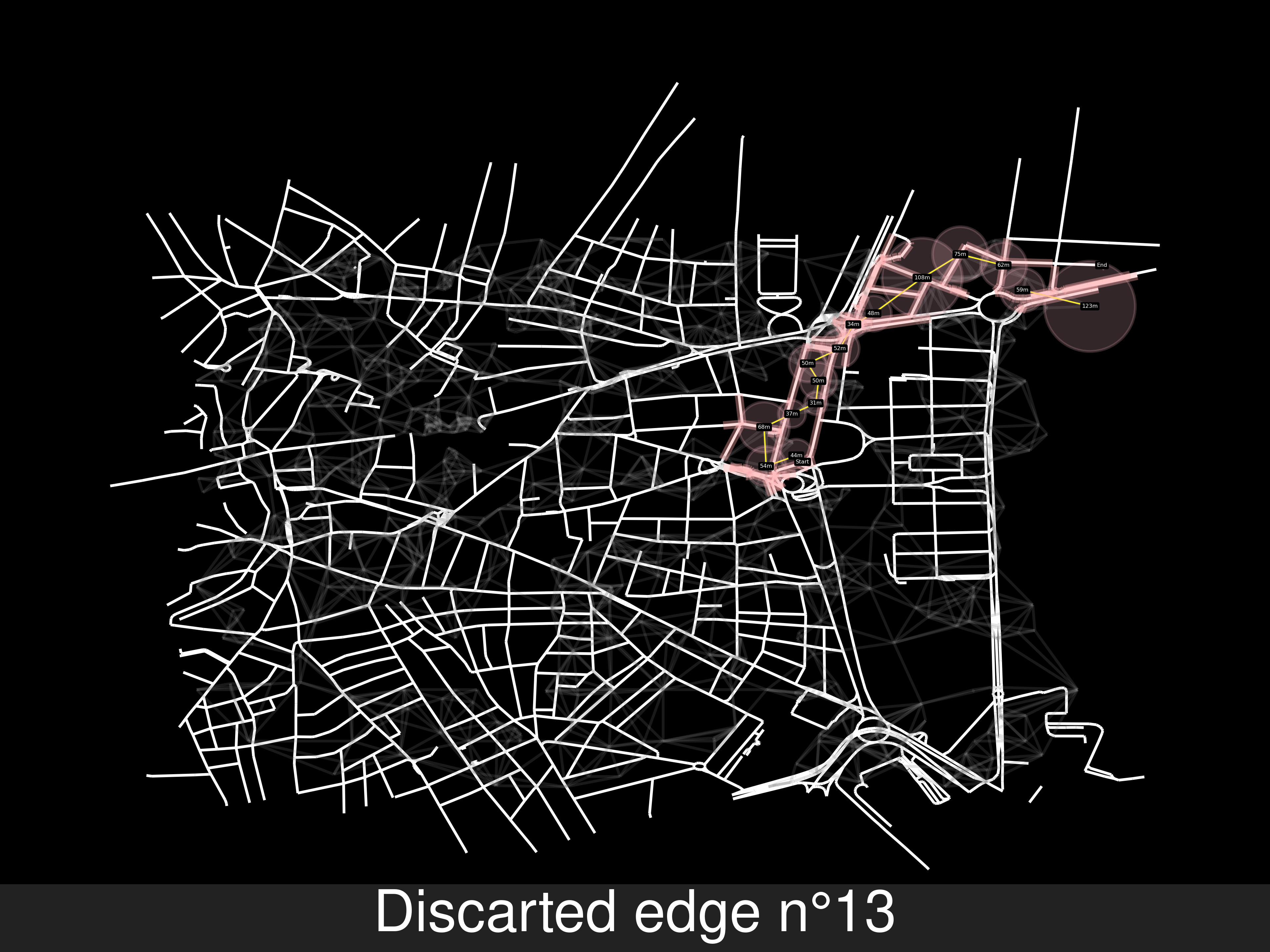
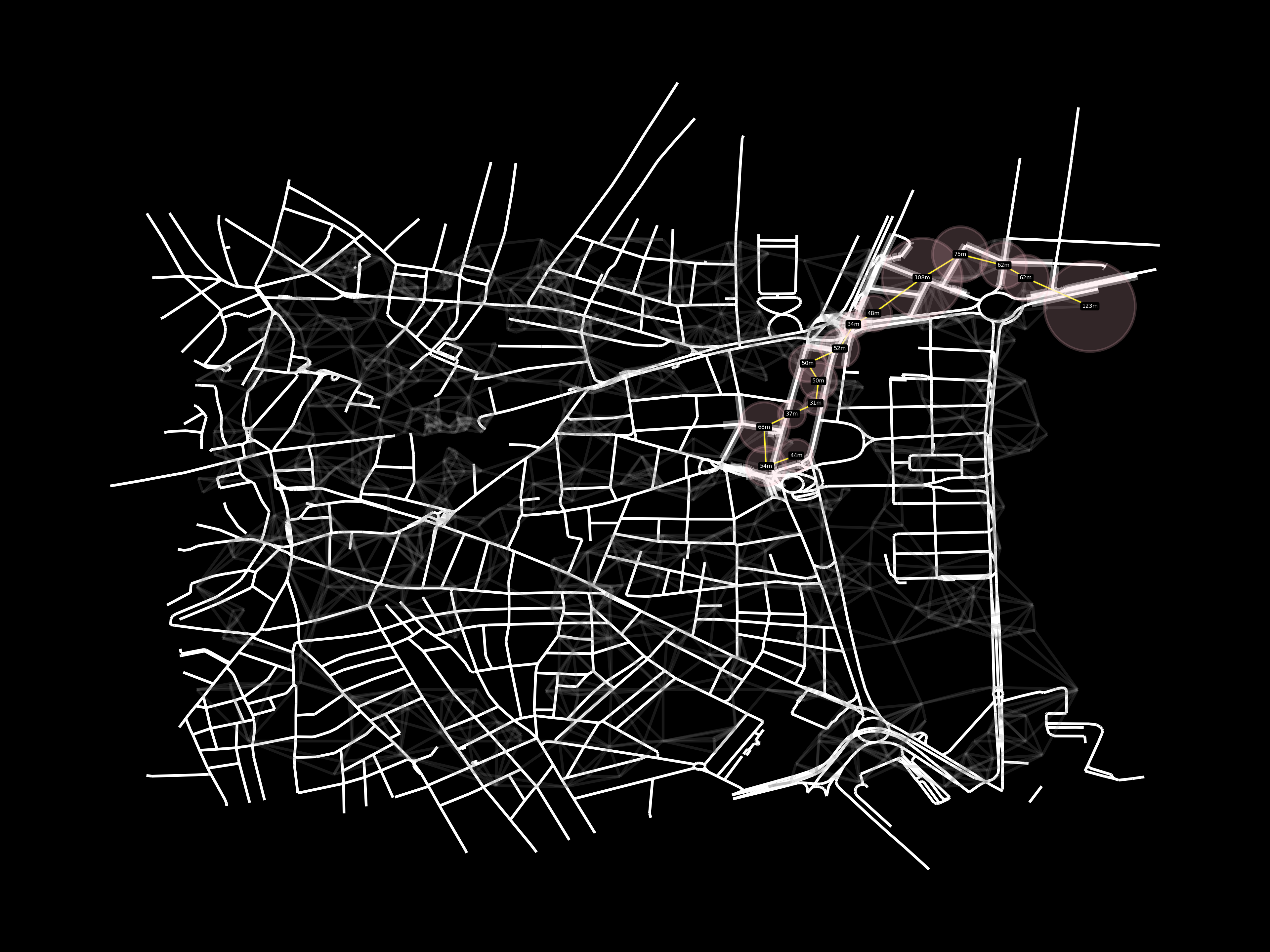
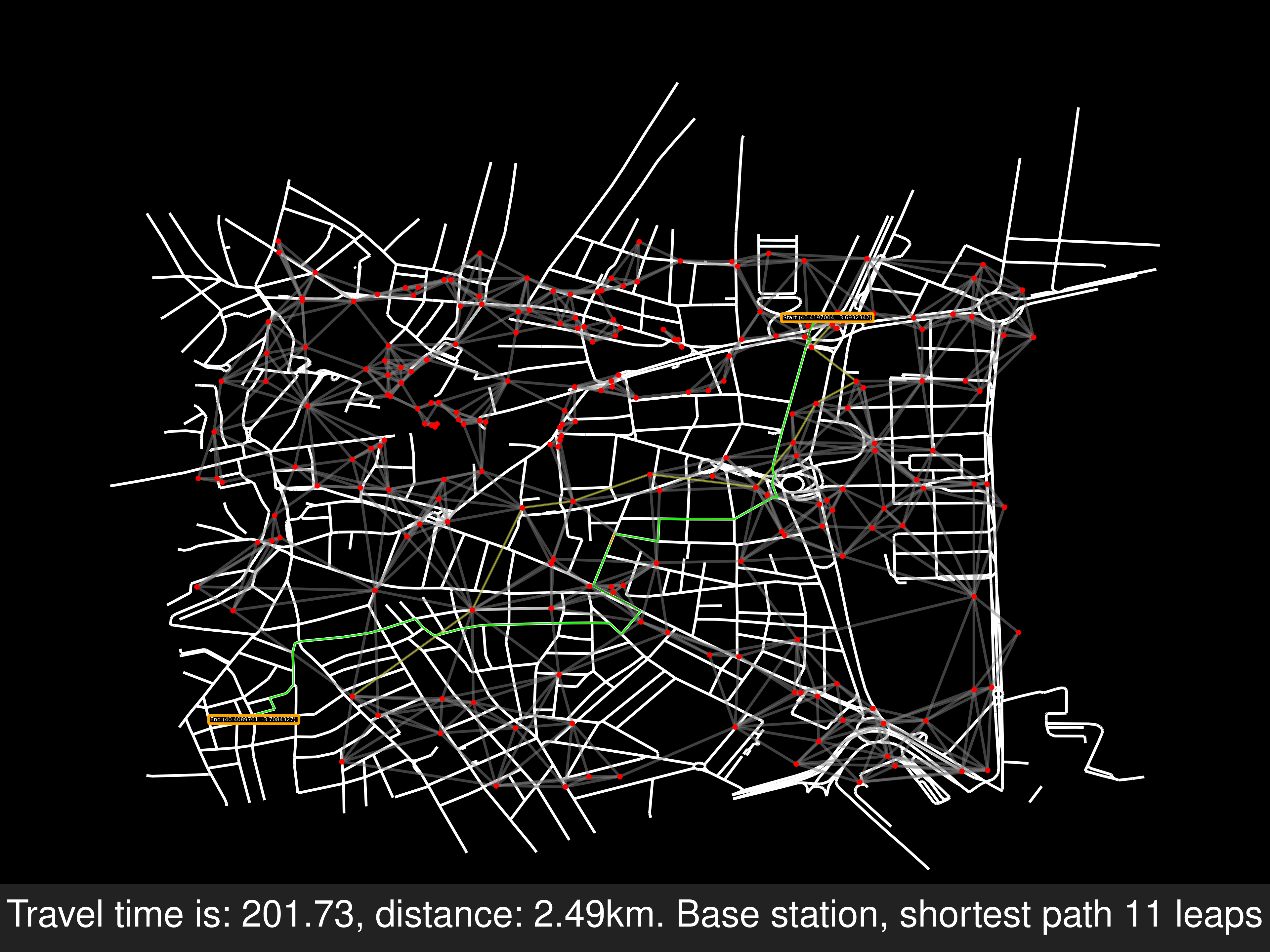
  3. Example C, another ok result

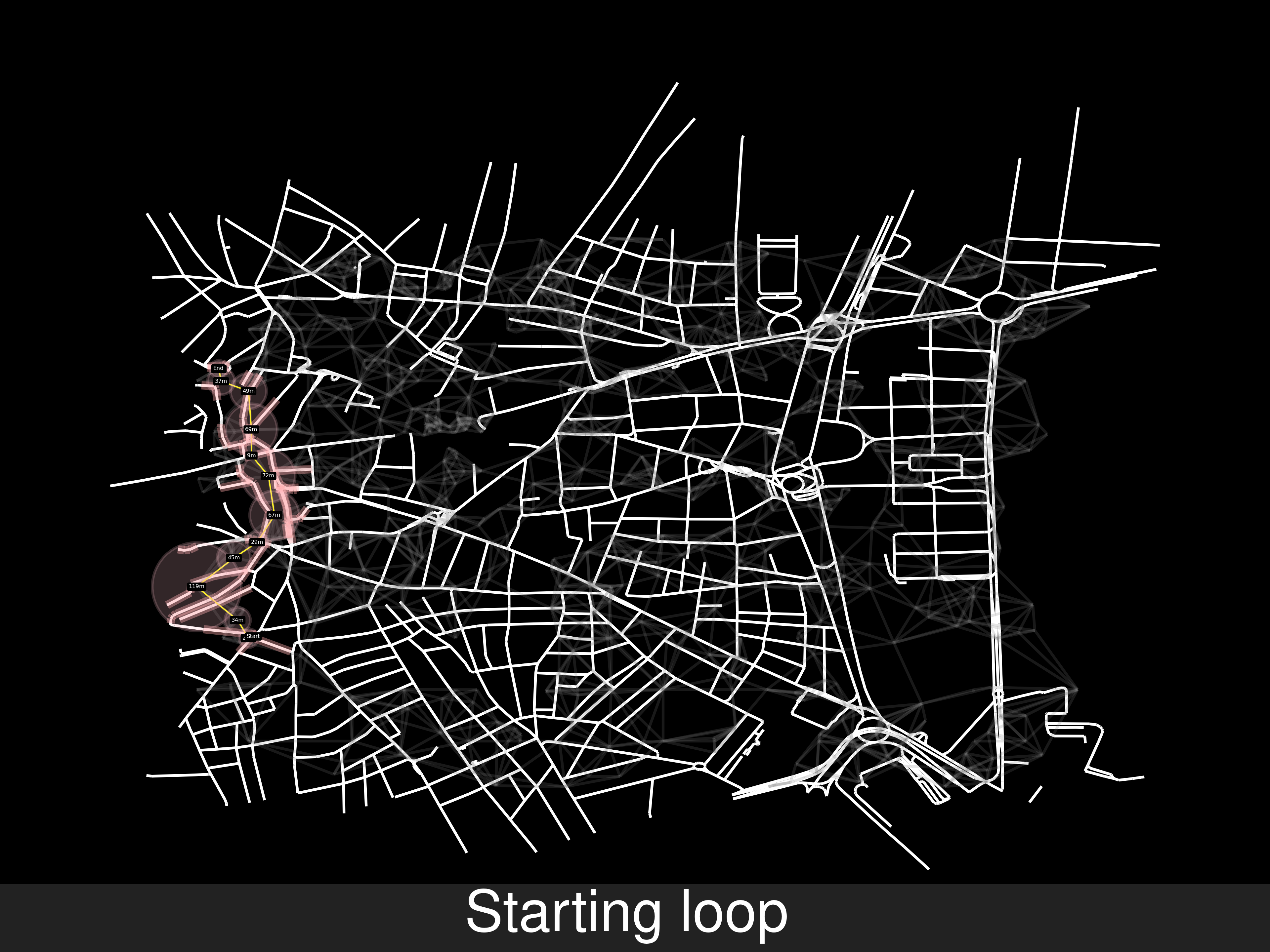
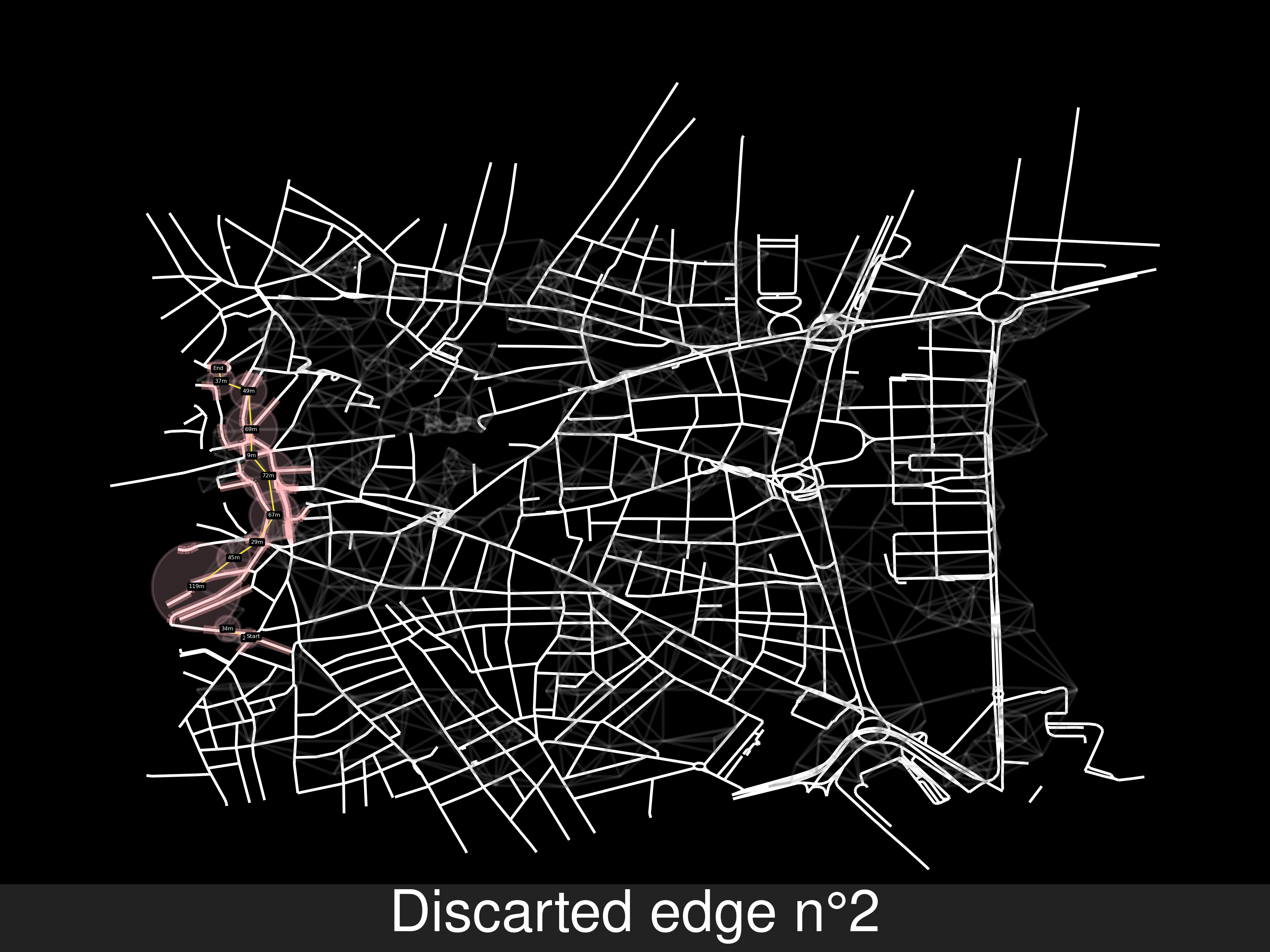
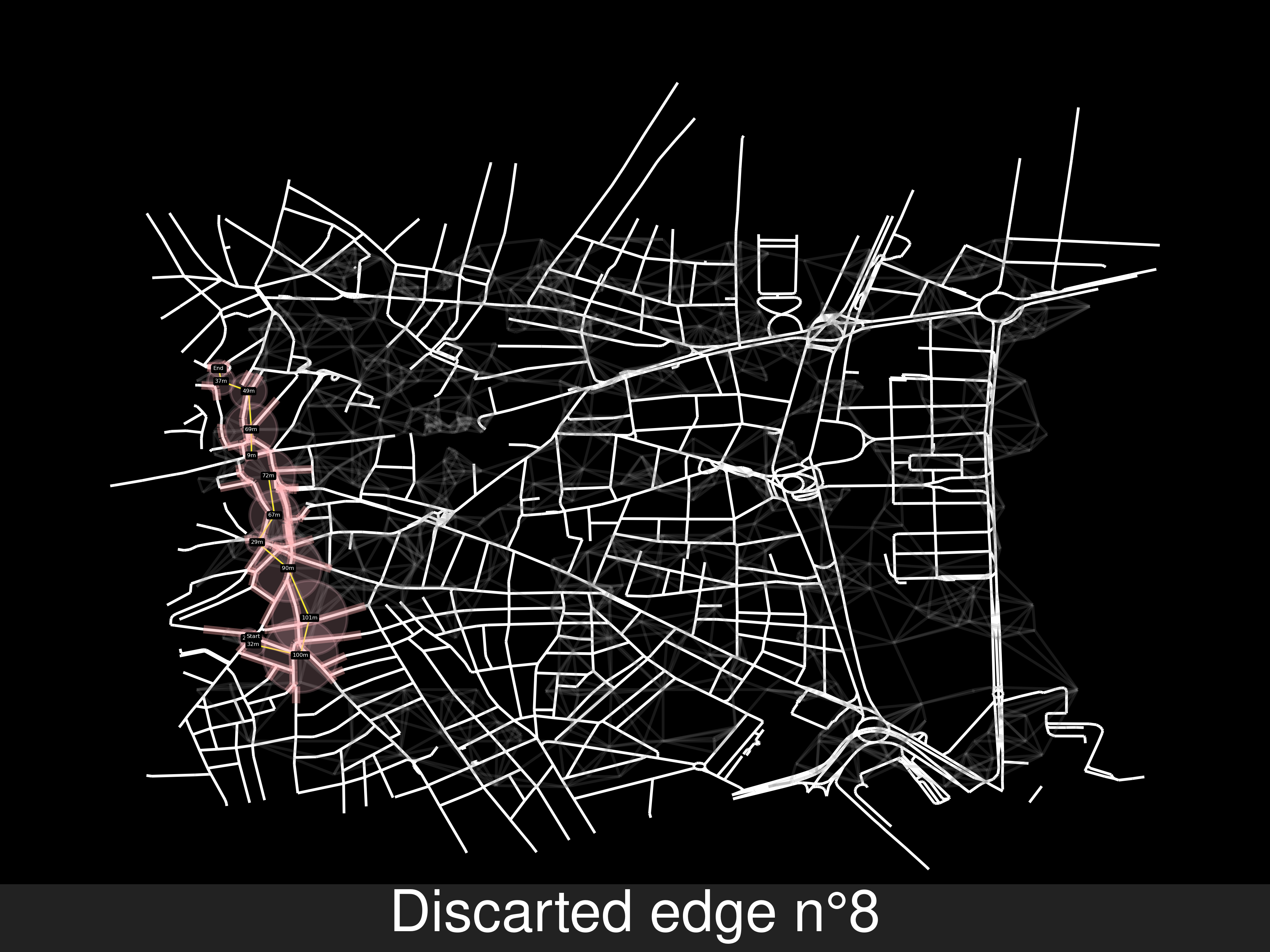
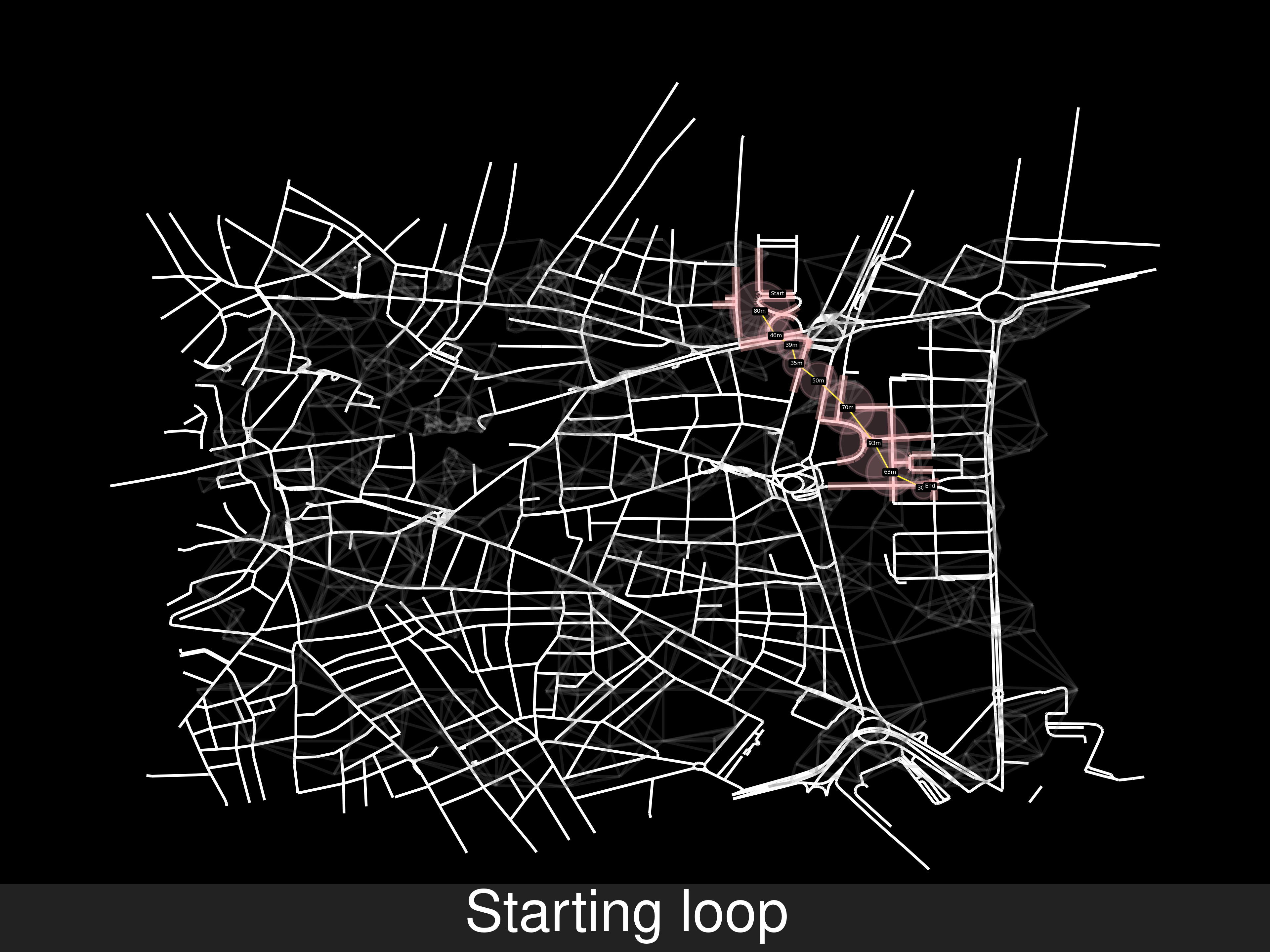
  4. Weird result:

  5. Increasing every cell’s range data0['range']=min1*2 if min1 < 50 else min1*1.3.

    Future solutions:

  6. Discard roads with no cell coverage
  7. Find shortest road path (Ignoring cells)
  8. Check for cells within the path.
  9. Repeat first step until the target is reached
  10. Choose the closer cells to each road as the cell graph

Semi-conclusion

  1. Conclusion from the algorithm: Once the entire map is covered, it’s slower trying to find a road path which fits the cell path than what we are doing, finding a cell path which contains a valid route. Hence, there’s an innherent trade off between shortest path in road (minimum distance or time) and cell’s required per travel.

  2. Conclusion from the data:

    1. It’s not realistic using SOI because it sets a circular range with tons of holes, which is rare in a high concentration of base stations, where this high number(cells/sqmeter) is due to the ammount of people/robustness to failure.
    2. We have to ignore the range of each cell, reported by opencellid
    3. It’s reasonable to think that in a city, every place is in coverage of at least 1 cells.

Voronoi - A better way to define a cell’s network and range

Using Voronoi

"... and then, all you've coded will be lost, like tears in the rain"