Last Modified: 2023-Jun-29

Remember to right click->"open image in new tab" for small images

Índice

  1. Voronoi representation
    1. Considerations
  2. Ok, looks cool what about the Algorithm
    1. The path solving would be performed like this
  3. How different is the new algorithm?

Voronoi representation

From the previous work, I conclude the algorithm for path solving was highly dependant on the cells graph. We need to connect each cell with all the of neighbouring cells, as with the sphere of influence moving throughout this cell graph is seen as us moving farther from the first cell and closer to the second one.

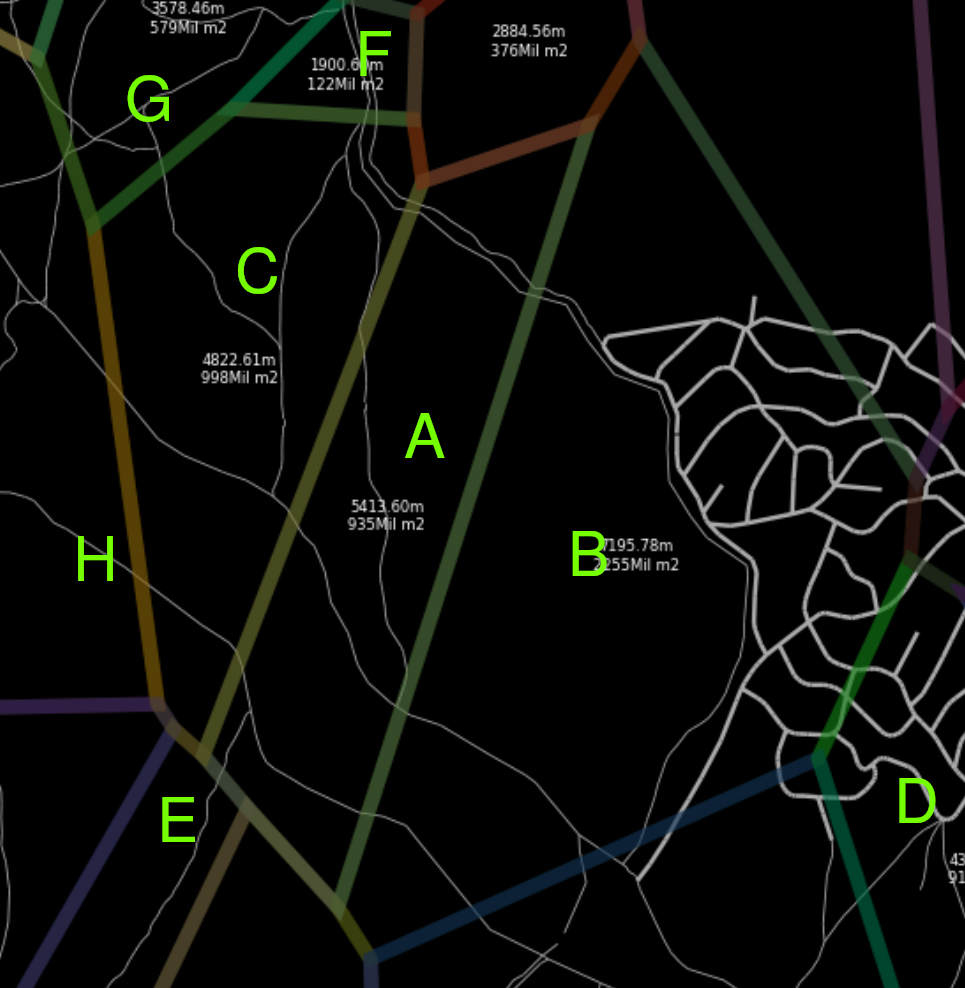
The Voronoi representation allows us to make a graph where each cell has an edge to each neighbouring cell. See image below, edges in gray, cells (red dots).

On the left, the voronoi regions(in blue) and their cells (red dots), on the right, in transparent gray the resulting graph’s edges

Many works also use Voronoi for modelling this kind of networks

Considerations

  1. 👍 I’m using plain Voronoi, not having into consideration the cell’s power, range field in opencellid database (unreliable field)
  2. 👍 Being inside a region of a cell means that most likely your phone will be connected to that tower cell
  3. 👎 Voronoi regions cover all of the map, there’s not any spot with no coverage, not true for remote places
  4. 👍👍👍👍👍👍👍 It looks good

Inside each V. region, the perimeter in meters and area in (area [m^2])/1000, and width of the ways by their kind (thicker primary,thinnest dirt ones)

Ok, looks cool what about the Algorithm

At first glance, using the same algorithm as before shortest path in cell graph gives us the same kind of problems as it did before.

  1. It seems pointless to check the roads inside a cell’s range more than one time, roads don’t move.
  2. The shortest path in the cell’s graph has zero value, we might as well pick a path with S shape and try to find a valid road path which satisfies reachability The shortest path in the cell’s graph would make sense if the landscape of the town was a grid or we have the guarantee a neighbouring cell has a road path which connects the roads under their coverage.

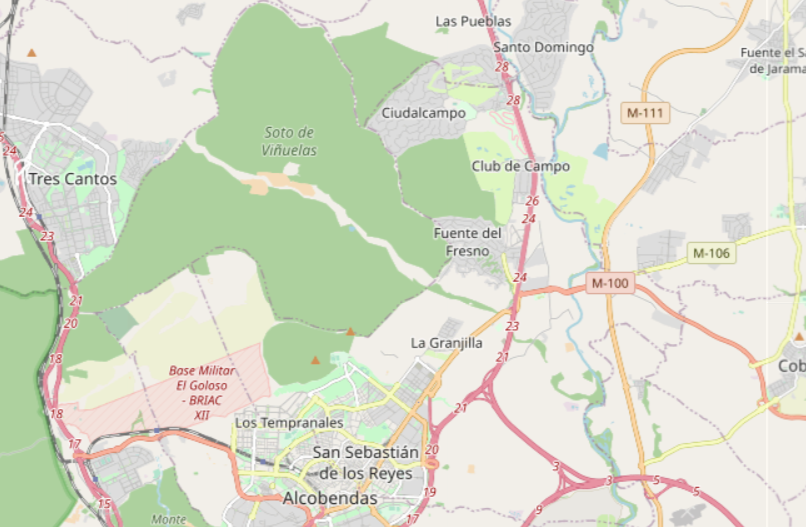
On the left, Manhattan, every road under every cell is reachable, on the right, Fuente de Fresno, Madrid, on which I will explain the new algorithm.

Using the old algorithm is just too slow, the cell’s graph give little information about how we can move from one cell to another by road.

Addressing both concerns, I came with this solution

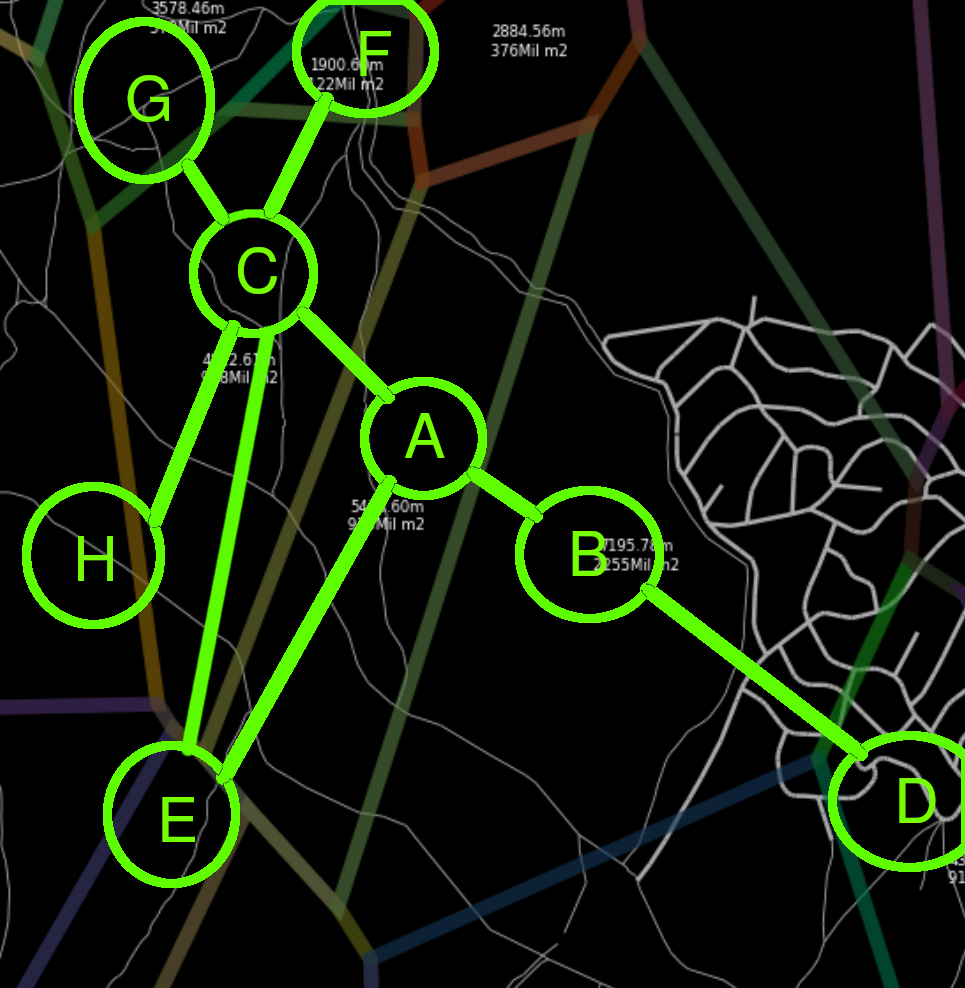
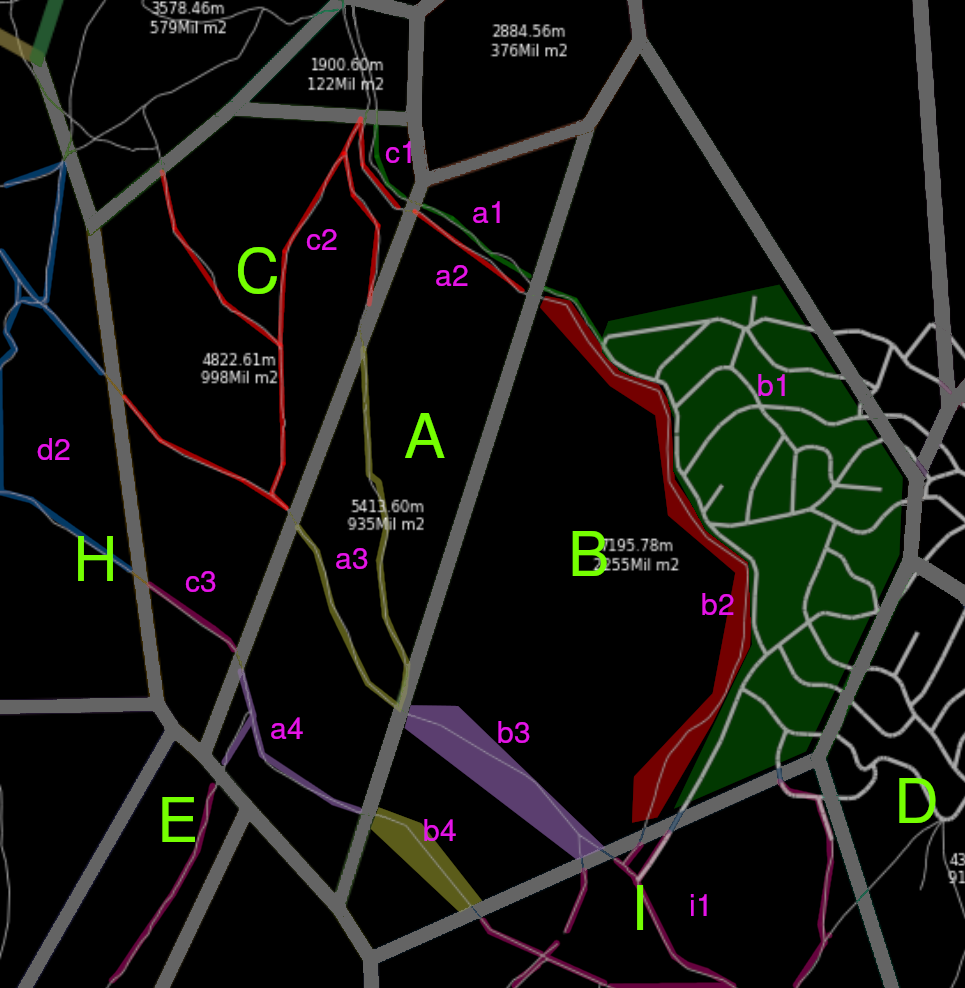
A voronoi region A contains 1 or more unreachable roads, each set of roads A1, A2, A3, A4 is connected or not to a neighbouring cell’s set of roads A1 - C1, A2 - C2, A3 - C2, , A4, C3.

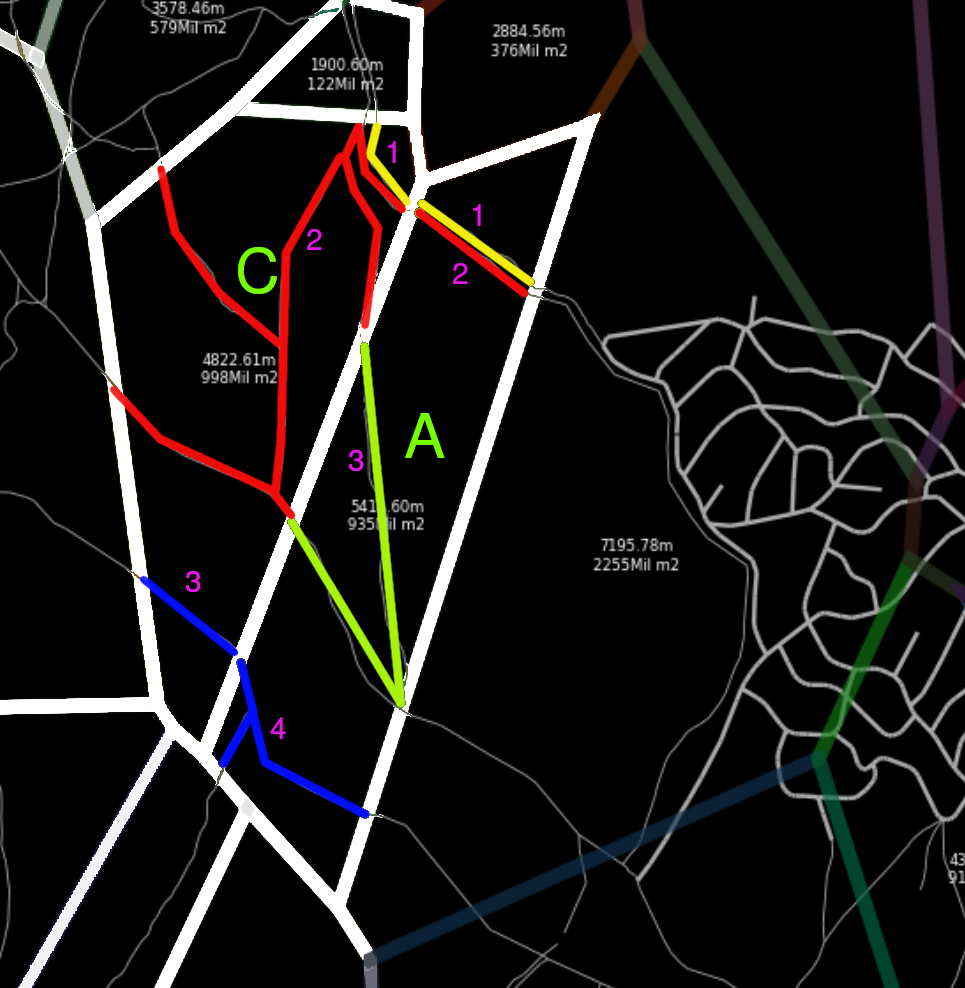
Hence, we can define a graph which only contains these sets of roads with the property that if the node Xi can reach Xj, hence, every road point from Xi can reach Xj.

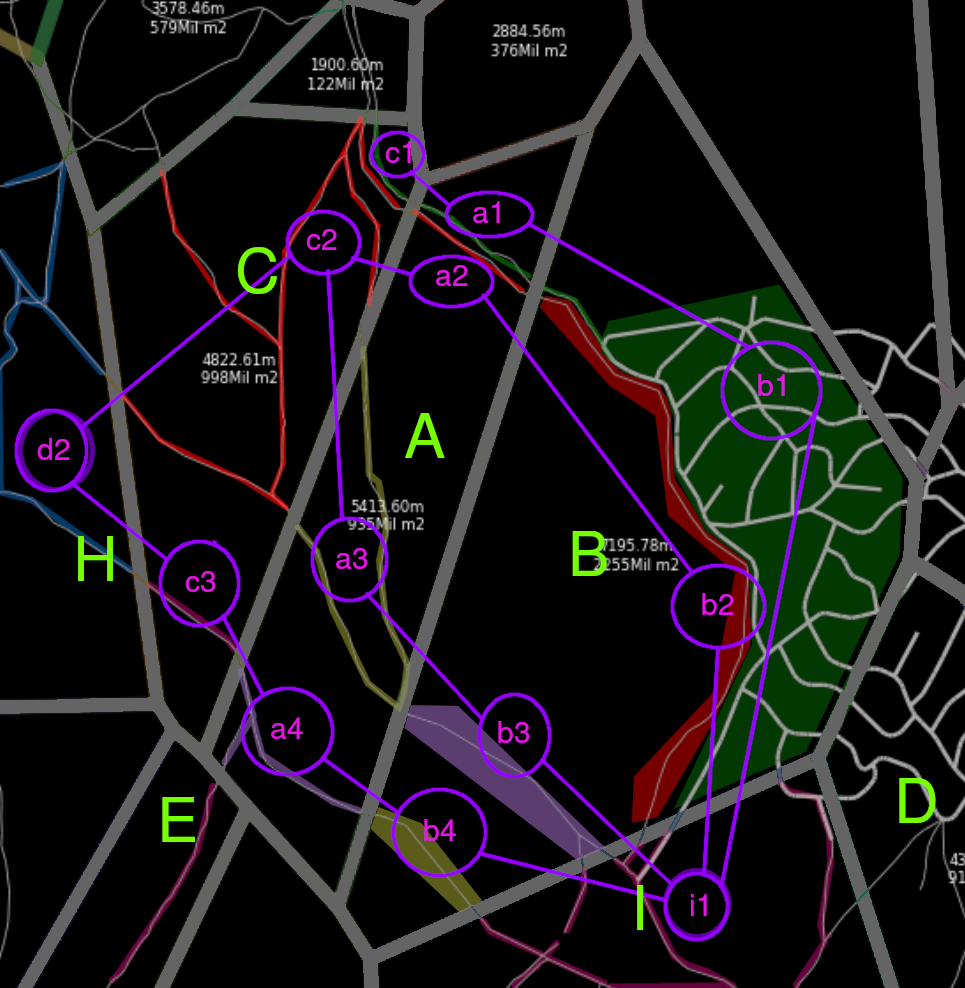
The path solving would be performed like this

For example, see P1 and P2. They are under the same cell: A, with the old algorithm we would end the search in the cell’s graph because the closer base station to P1 is the same as P2.

Using this new algorithm:

  1. From P1 we get the set of roads which contains it -> A3

  2. From P2 we get the set of roads which contains it -> A4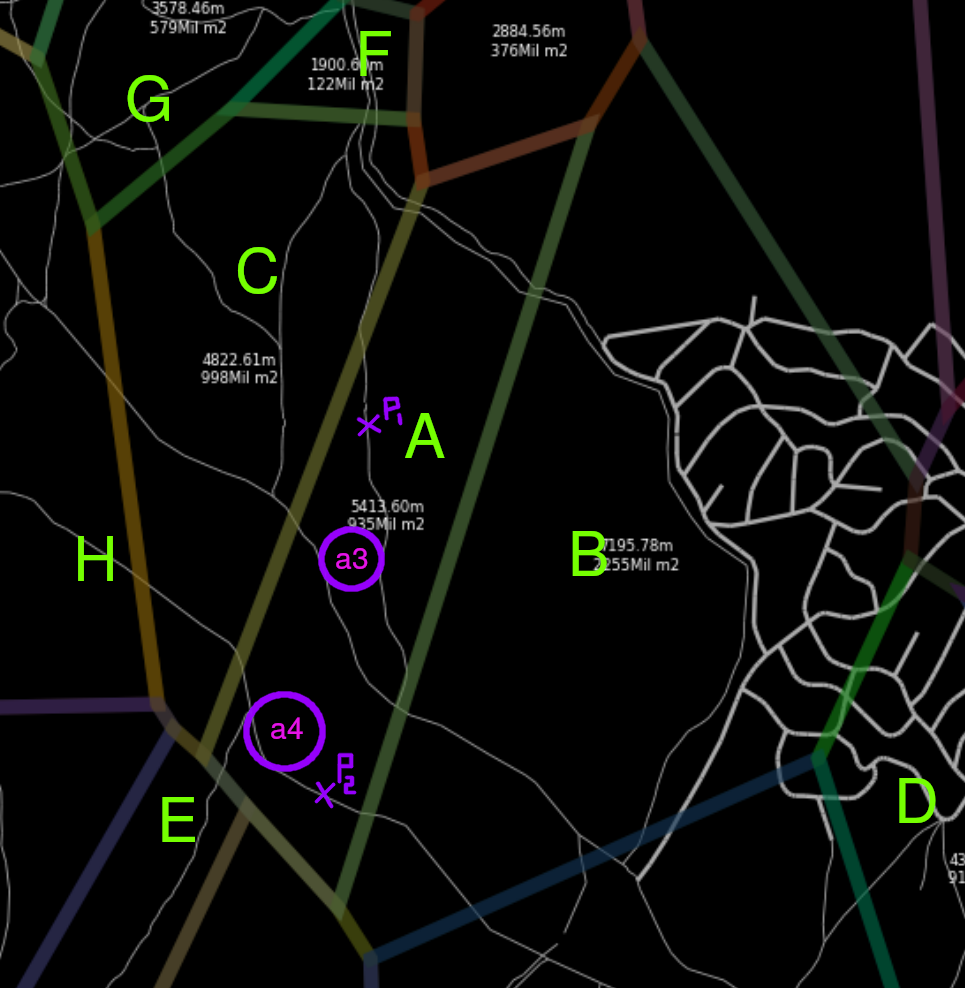

  3. We obtain a path between A3 and A4. i.e.(Using A*) A3,C2,D2,C3,A4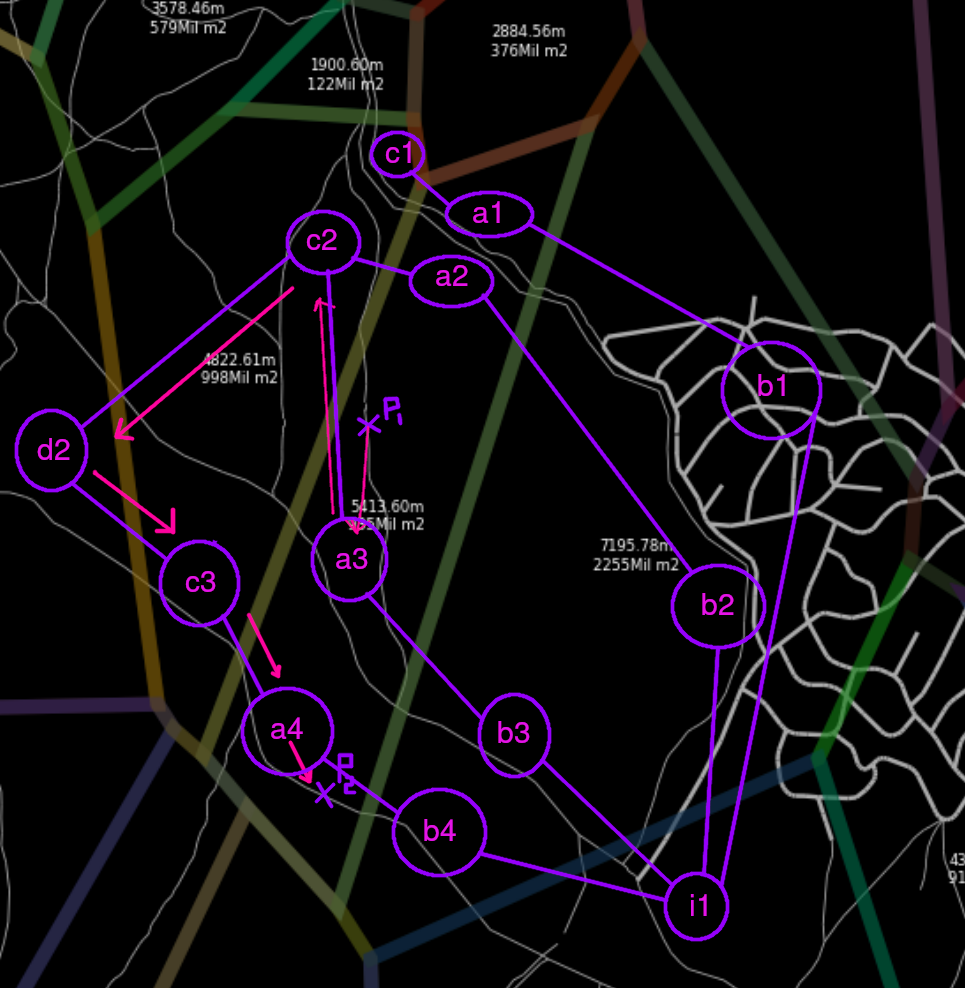

  4. We join the set of roads and perform the searching algorithm (i.e. A*) and we obtain the shortest path in road, painted in green.

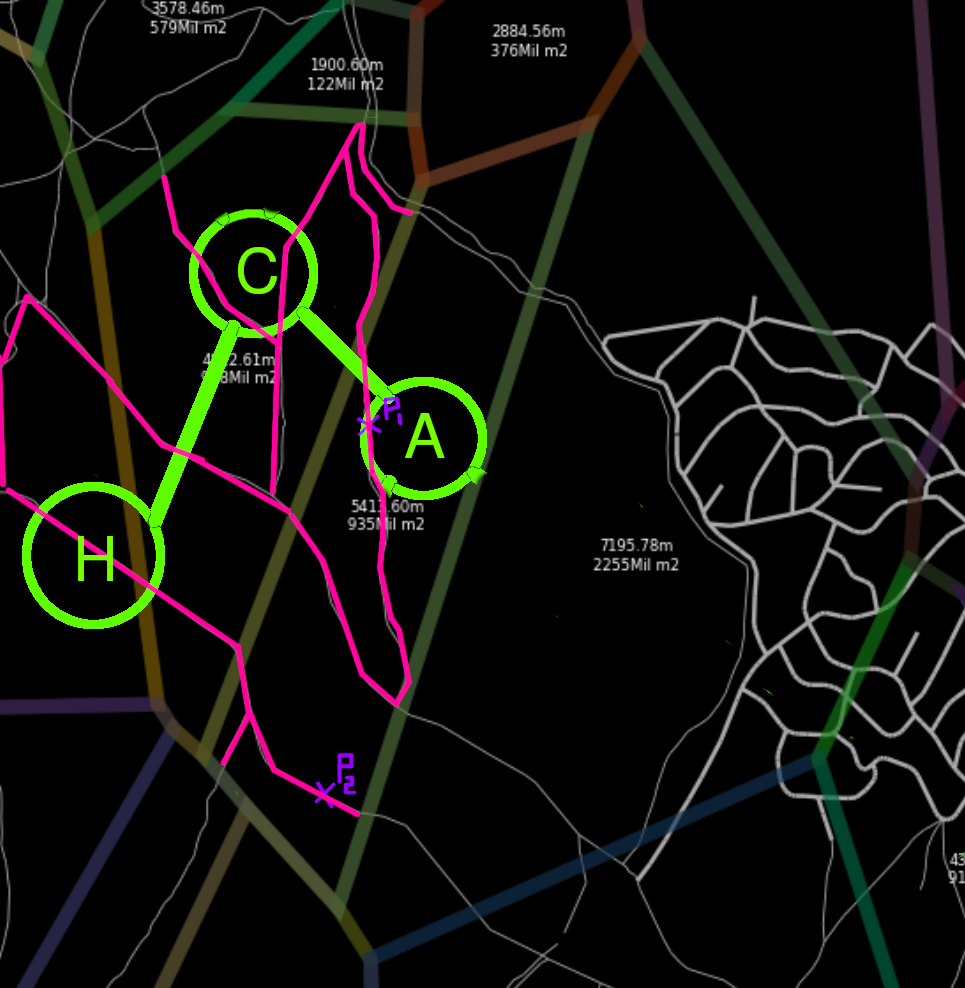
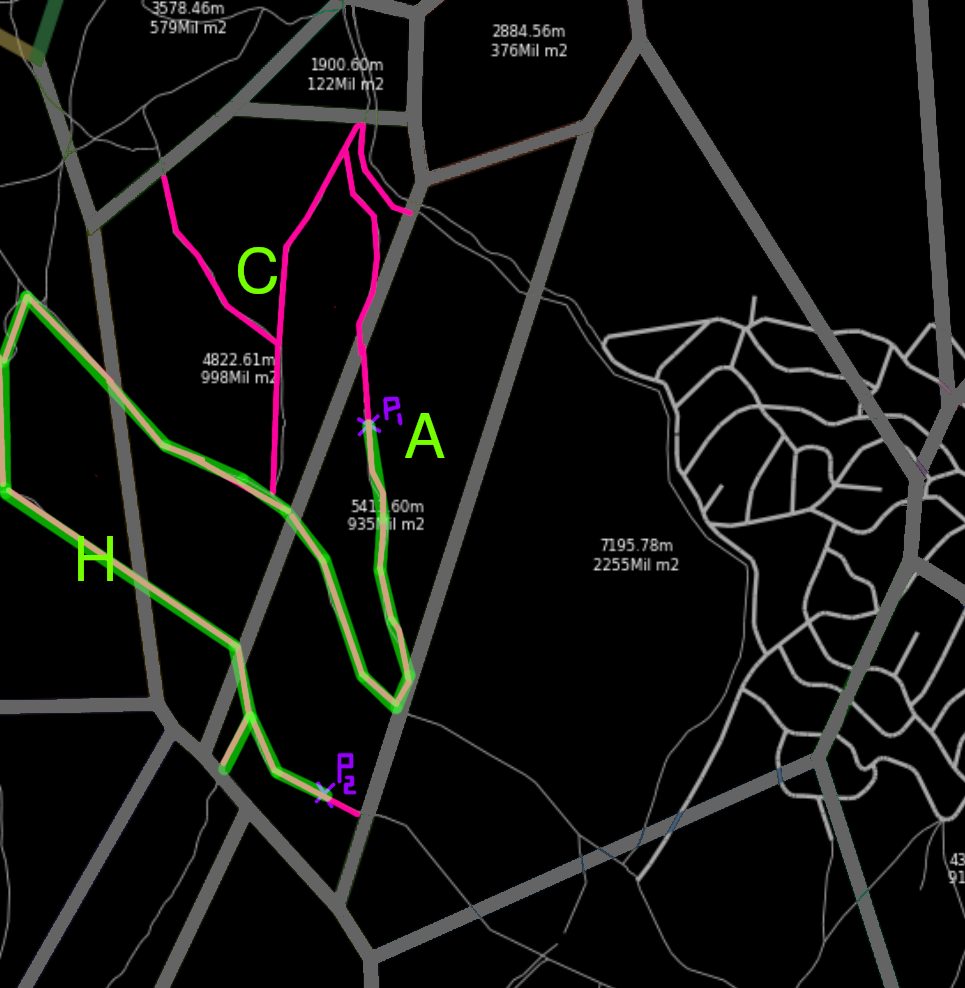
In step 3, using a shortest path solving we are guaranteeing that the resuling path uses the less ammount of jumps between cells, this is not guaranteed if we solve the shortest path only having into consideration the road network.

How different is the new algorithm?

Because this algorithms seeks for the less ammount of jumps between cells. We have to compare what’s the tradeoff against the shortest path by road (ignoring cells). Simulating shortest path for two random points:

distances nsamples Cell Hops New/Old [%] Cells Used New/Old Travel Time New/Old max TT New/Old Time of Compute New/Old max ToC New/Old CellSeconds
0 < 1km 1178 95.02 1.01 1.15 26.19 3.66 386.61 1.33
1 km <= 2km 1766 86.21 0.92 1.24 10.95 2.26 54.30 1.23
2 km <= 3km 1270 77.43 0.83 1.36 8.90 1.31 66.31 1.19
3 km <= 5km 2061 68.35 0.74 1.46 7.55 1.17 80.62 1.10
5 km <= 10km 2595 60.47 0.67 1.60 3.99 1.22 52.98 1.07
10 km <= 15km 1083 54.83 0.60 1.62 3.75 1.58 86.20 0.94
15km or more 899 50.09 0.53 1.39 2.57 1.91 40.59 0.71

Fields: The stats New/Old are the division between results with this algorithm and A* _Although in the pictures there’s a label Dijkstra, it’s A*

  • Distances: Distance of the path A* between points P1 and P2
  • nsamples: Number of samples per distance range
  • Cell Hops: Times the path changes from one cell to another (i.e. A1,A2,A1,A3,A2 → 4 hops)
  • Cells Used: Unique set of Cell Hops (i.e. A1,A2,A3 → 3 cells used)
  • Travel Time: Total travel time of the path
  • max TT: maximum travel time, “worst case”
  • Time of Compute: Time needed for finding the shortest path:
    • Old: Only A* into consideration
    • New: Time needed for the path in the cell graph and the in the subset road graph
  • CellSeconds: Metric inspired on the energy unit [KWh]: (NewCellsUsed*NewTravelTime)/(OldCellsUsed*OldTravelTime) i.e. 4 cells for 300 seconds = 1200 Cs ⇔ 16 cells for 75 seconds = 1200 Cs Few example of zones:
  • Madrid Hortaleza SanBlas Tetuan :
distances nsamples Cell Hops New/Old [%] Cells Used New/Old Travel Time New/Old max TT New/Old Time of Compute New/Old max ToC New/Old CellSeconds
0 < 1km 25 93.14 0.99 1.50 9.36 6.68 112.58 1.55
1 km <= 2km 97 92.45 0.99 1.66 10.95 2.49 38.65 2.54
2 km <= 3km 128 79.58 0.85 1.57 8.11 1.10 14.28 1.49
3 km <= 5km 386 68.57 0.75 1.61 7.55 1.02 16.09 1.29
5 km <= 10km 1034 56.71 0.64 1.71 3.69 1.06 11.25 1.10
10 km <= 15km 433 49.14 0.56 1.77 3.04 1.52 4.54 1.01
15km or more 33 46.01 0.54 1.86 2.46 2.13 4.61 1.01

  • Madrid Centro:
distances nsamples Cell Hops New/Old [%] Cells Used New/Old Travel Time New/Old max TT New/Old Time of Compute New/Old max ToC New/Old CellSeconds
0 < 1km 84 91.43 1.02 1.52 26.19 6.65 386.61 3.85
1 km <= 2km 210 82.64 0.89 1.65 9.58 1.66 54.30 1.73
2 km <= 3km 331 77.52 0.85 1.65 8.90 1.23 66.31 1.57
3 km <= 5km 762 65.40 0.72 1.58 5.83 1.11 41.10 1.17
5 km <= 10km 878 58.66 0.66 1.65 3.02 1.27 32.34 1.11
10 km <= 15km 22 50.87 0.57 1.56 2.03 1.47 3.24 0.96

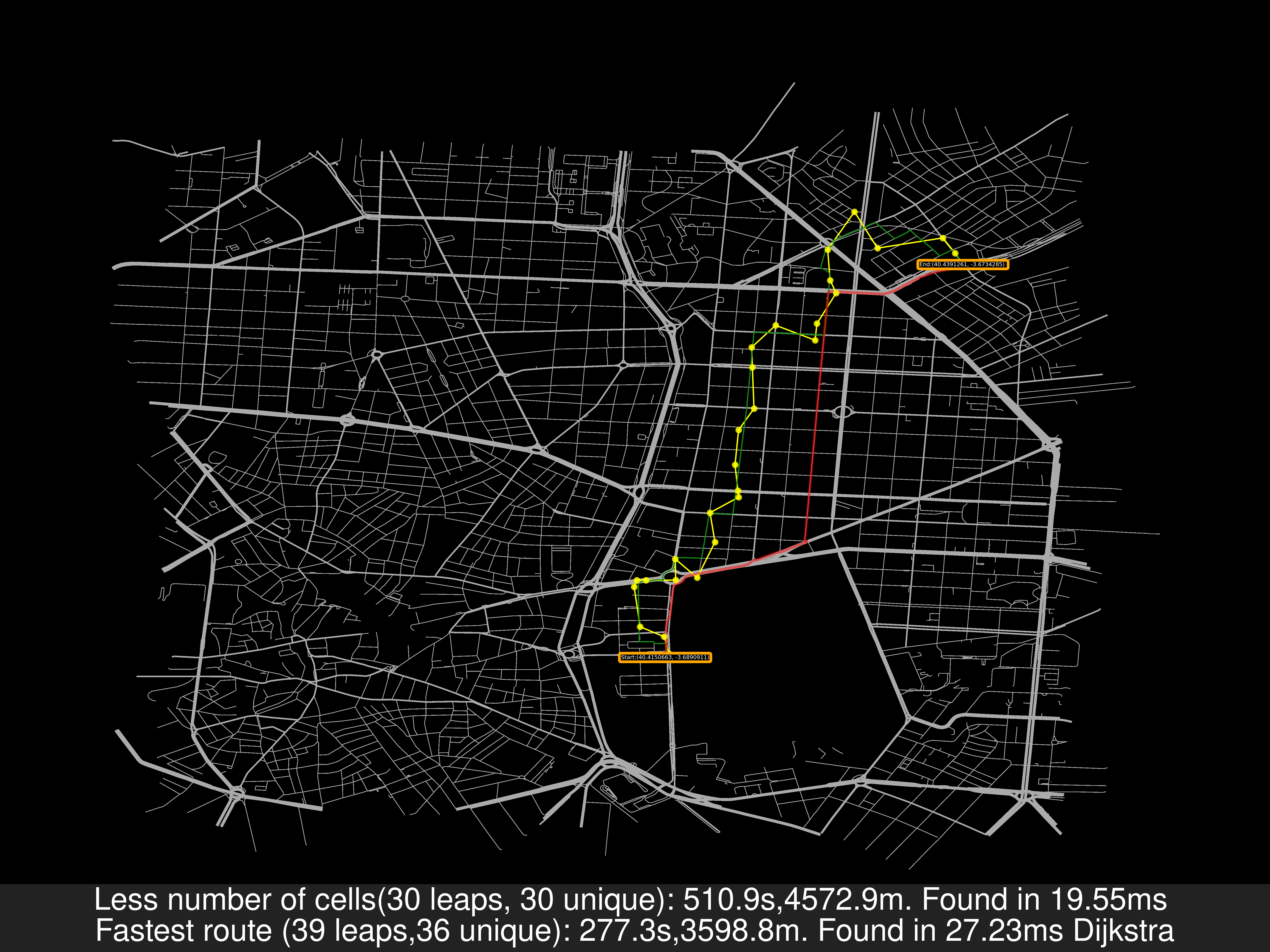
  • Alcobendas:
distances nsamples Cell Hops New/Old [%] Cells Used New/Old Travel Time New/Old max TT New/Old Time of Compute New/Old max ToC New/Old CellSeconds
0 < 1km 164 90.97 0.94 1.10 2.22 3.26 39.94 1.01
1 km <= 2km 447 82.88 0.87 1.20 7.24 1.75 44.99 1.05
2 km <= 3km 604 76.30 0.80 1.24 2.67 1.08 8.66 0.99
3 km <= 5km 719 69.71 0.74 1.29 3.73 1.29 80.62 0.95
5 km <= 10km 220 59.73 0.64 1.31 2.25 1.45 7.31 0.83

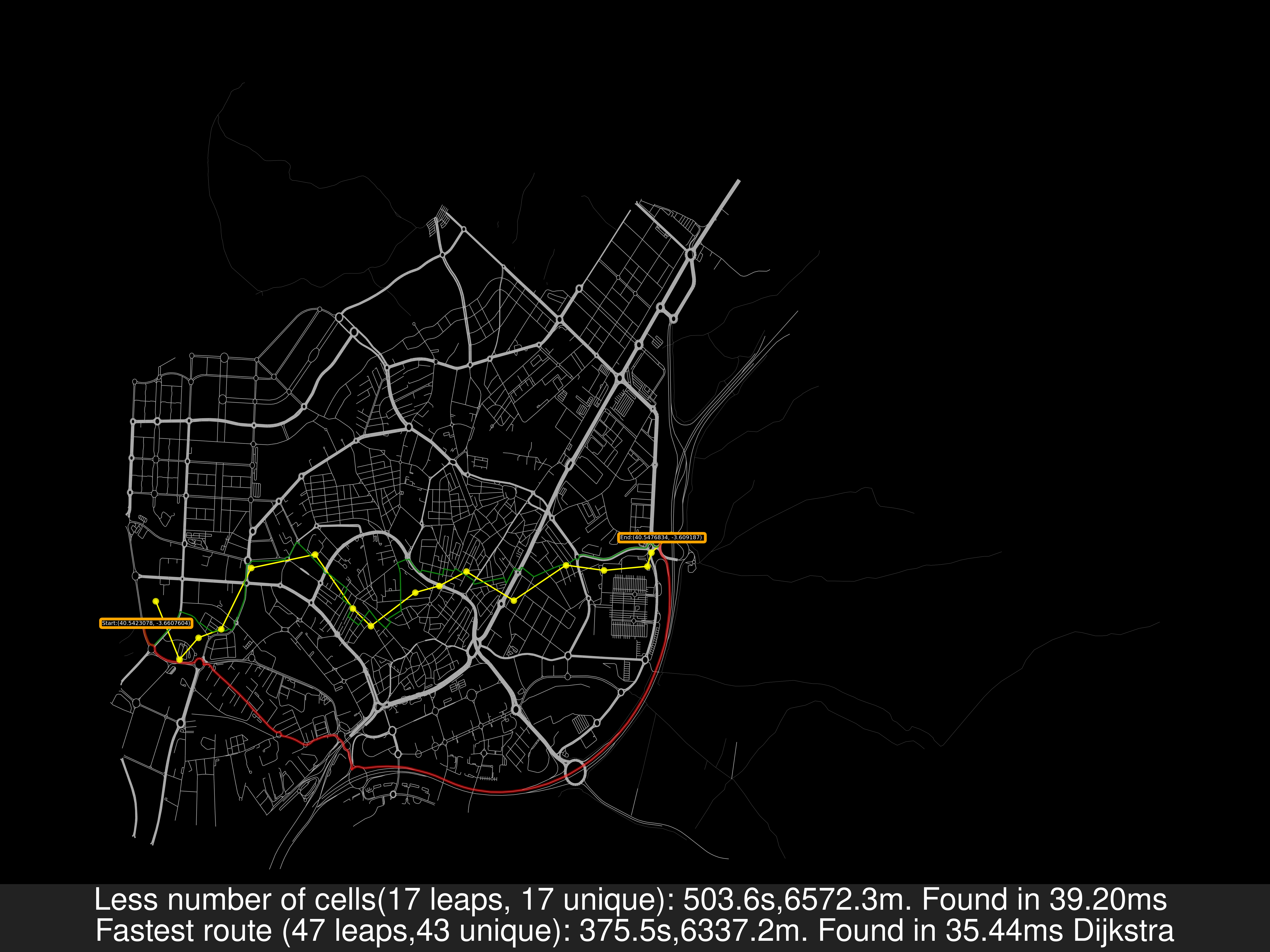
  • Alcobendas Small:
distances nsamples Cell Hops New/Old [%] Cells Used New/Old Travel Time New/Old max TT New/Old Time of Compute New/Old max ToC New/Old CellSeconds
0 < 1km 887 96.33 1.02 1.11 5.07 3.38 60.09 1.15
1 km <= 2km 951 87.60 0.94 1.12 2.93 2.64 51.18 1.07
2 km <= 3km 132 78.12 0.86 1.08 1.57 2.76 12.46 0.95
3 km <= 5km 7 76.47 0.84 0.94 1.12 2.68 3.39 0.89

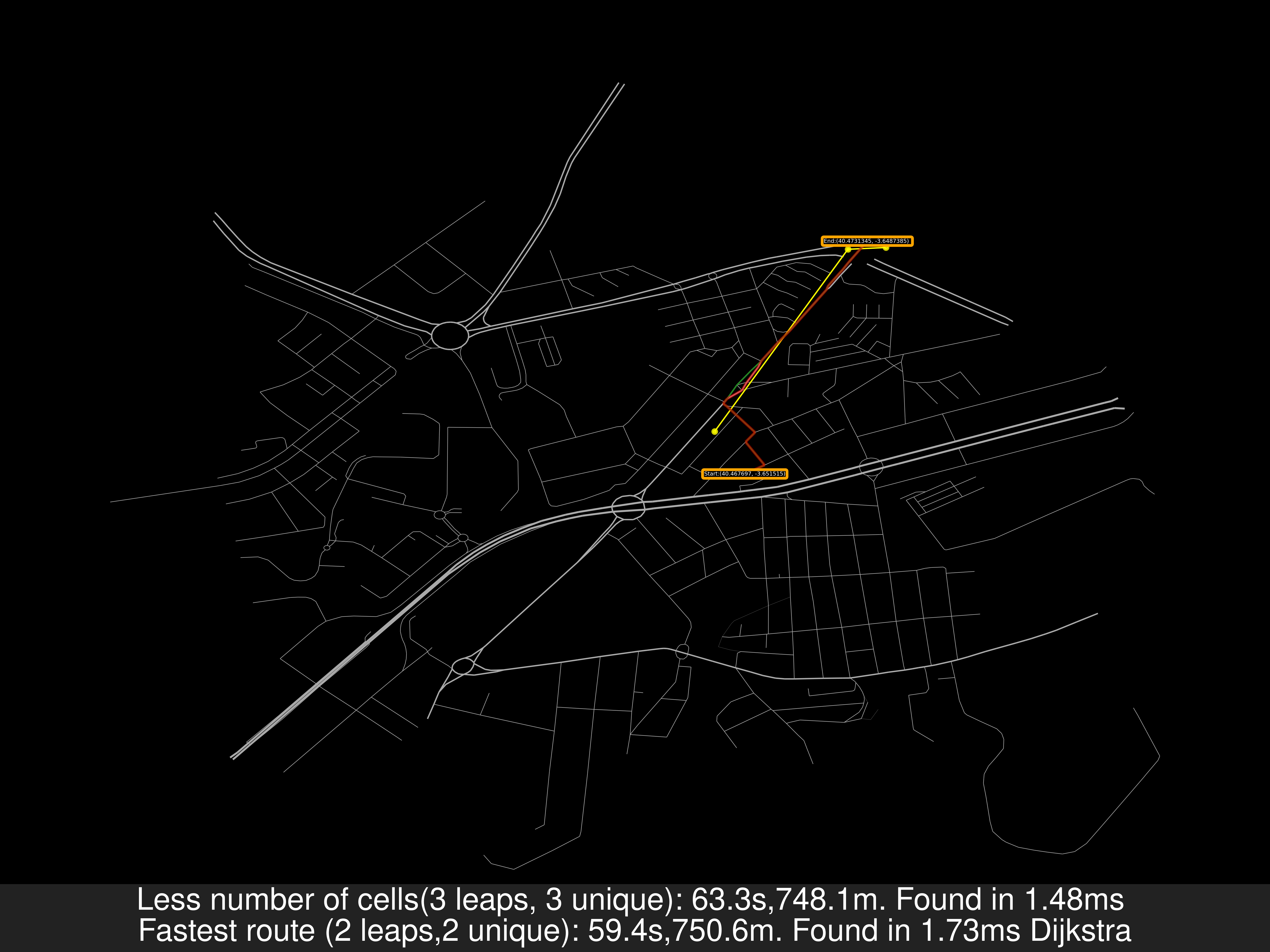
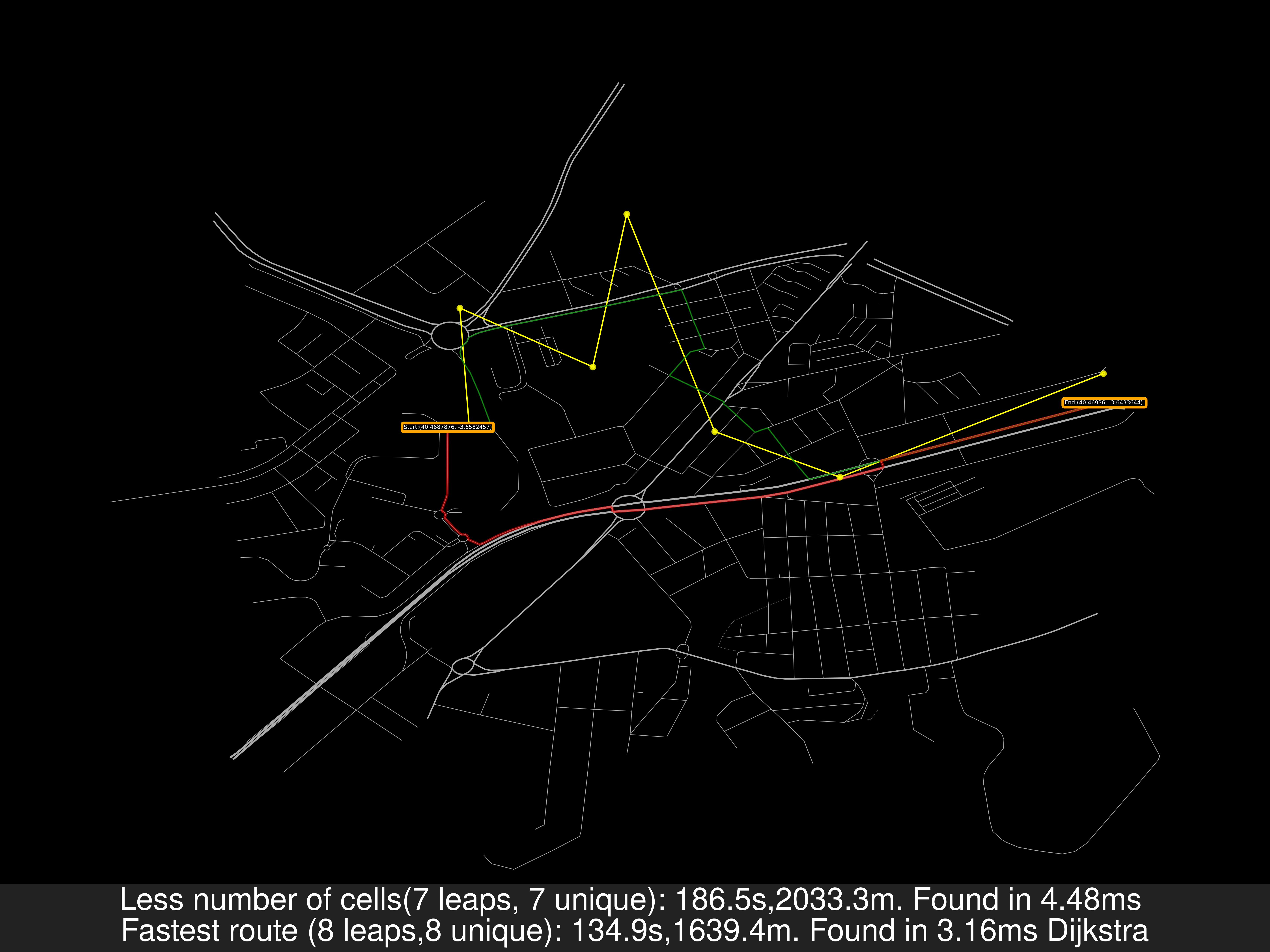
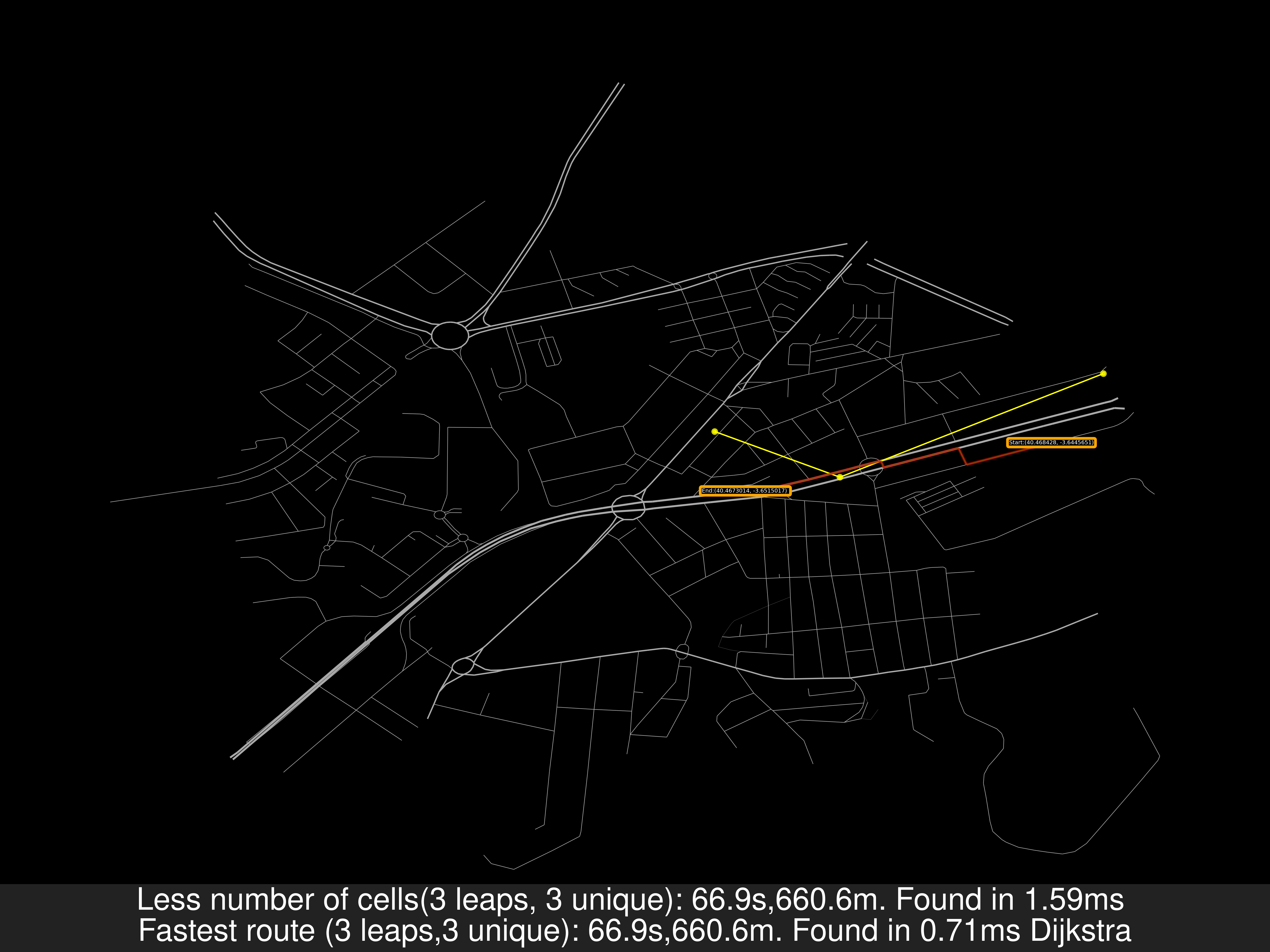
  • Alcobendas TresCantos FuentedelFresno:
distances nsamples Cell Hops New/Old [%] Cells Used New/Old Travel Time New/Old max TT New/Old Time of Compute New/Old max ToC New/Old CellSeconds
0 < 1km 18 86.67 0.93 1.16 1.98 3.12 8.69 1.06
1 km <= 2km 61 91.43 0.96 1.15 3.58 1.73 13.17 1.14
2 km <= 3km 75 81.24 0.87 1.25 2.88 1.19 8.09 1.10
3 km <= 5km 187 74.38 0.79 1.31 4.10 1.21 8.71 1.03
5 km <= 10km 463 72.67 0.77 1.41 3.99 1.37 52.98 1.07
10 km <= 15km 628 58.90 0.62 1.51 3.75 1.63 86.20 0.90
15km or more 866 50.25 0.53 1.37 2.57 1.90 40.59 0.70

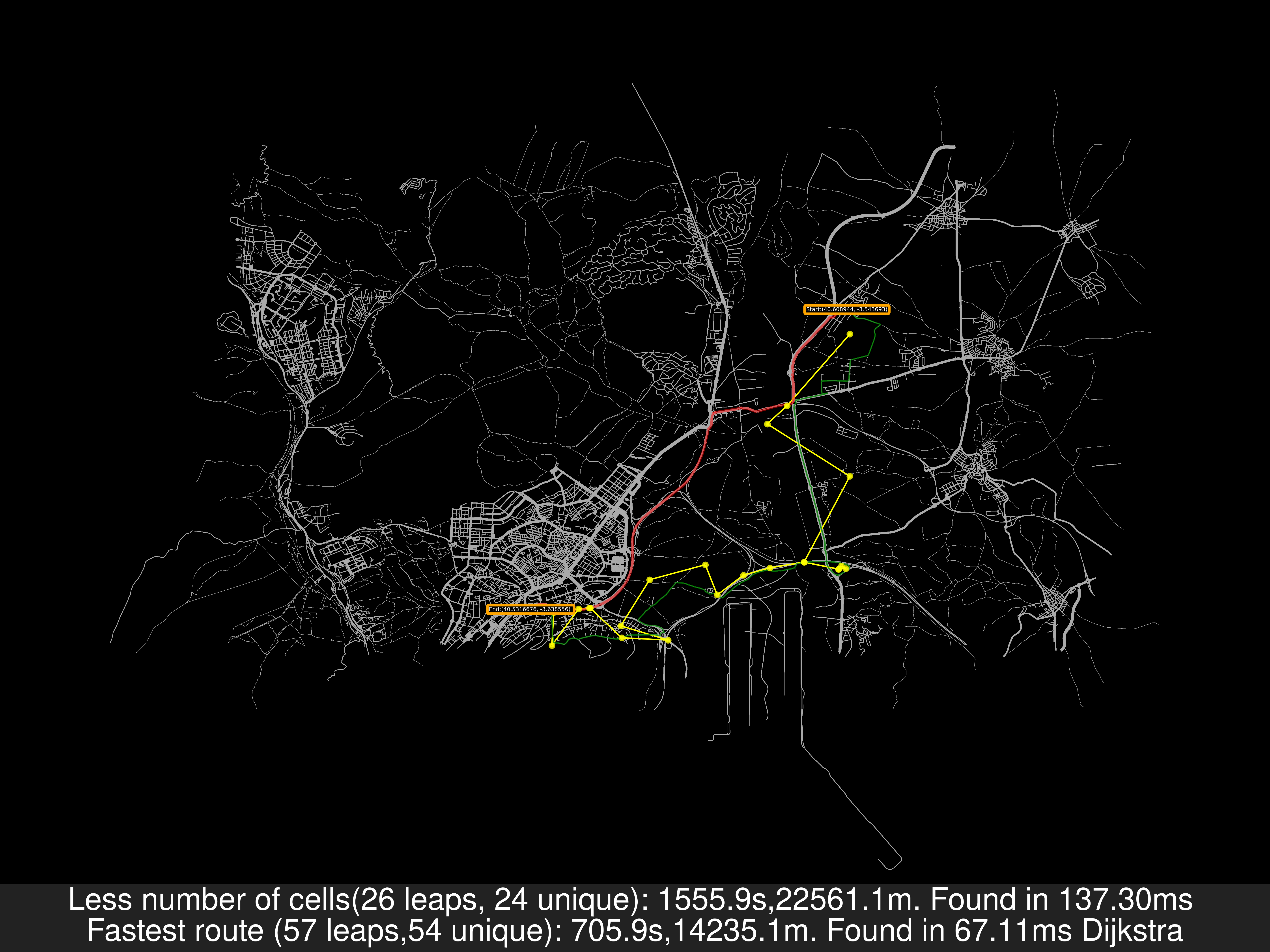
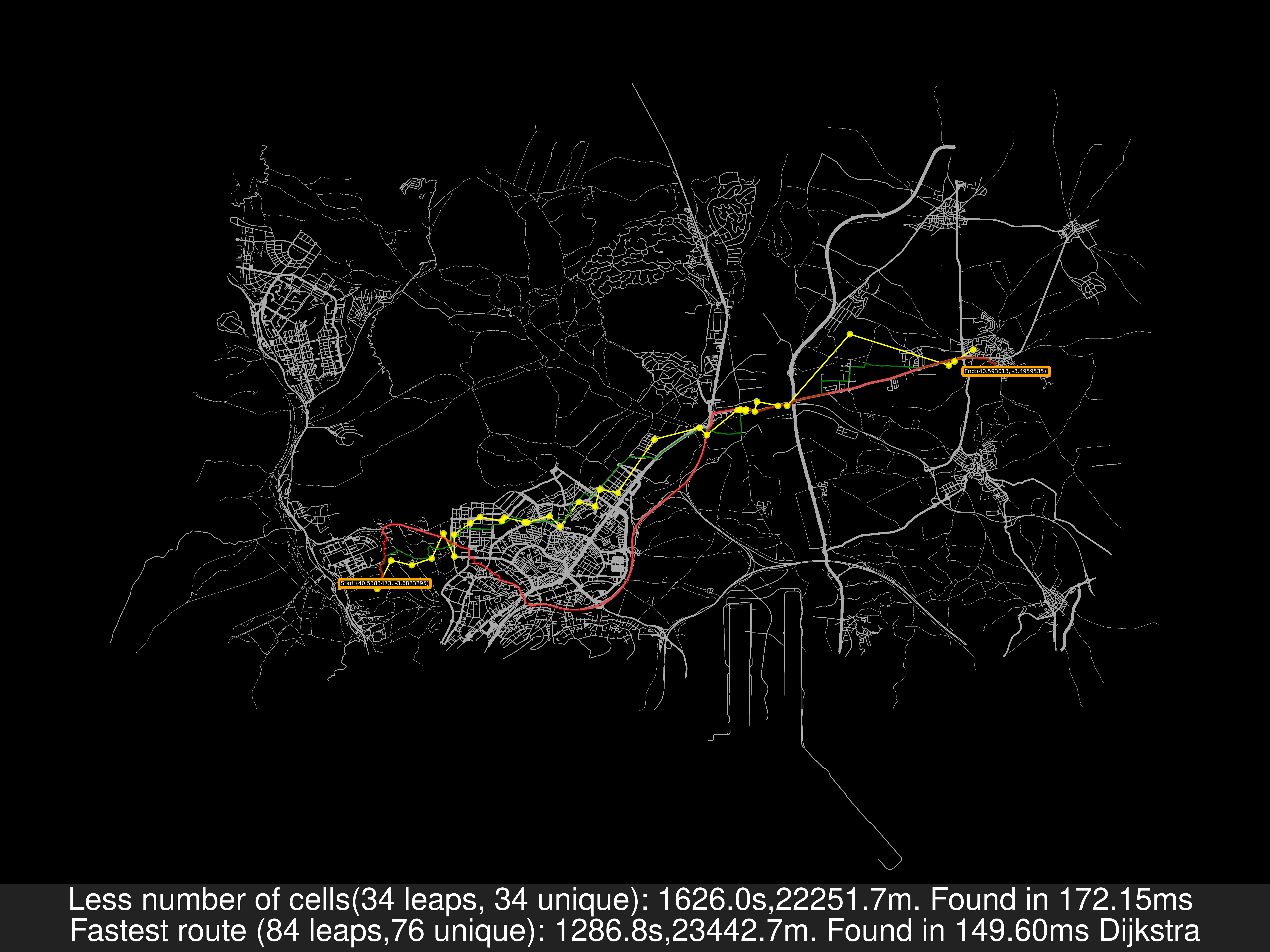
As a remainder: In the previous image, the travel distance is greater in the Less cells case but the travel time is smaller. That’s because for the road’s speed I’ve used uber movement data

"... and then, all you've coded will be lost, like tears in the rain"